
题目列表(包括答案和解析)
| a+b |
| 2 |
| a-b |
| 2 |
| (a+b-2)-(a+b-2ab) |
| 2 |
| (a+b-2)-(a+b-2ab) |
| 2 |
阅读并解答下列问题:我们熟悉两个乘法公式:①( +b)2=
+b)2= 2+2
2+2 b+b2;②(
b+b2;②( -b)2=
-b)2= 2-2
2-2 b+b2.现将这两个公式变形,可得到一个新的公式③:
b+b2.现将这两个公式变形,可得到一个新的公式③: b=(
b=(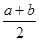 )2-(
)2-(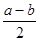 )2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
)2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
例如:因式分解:( b-1)2+(
b-1)2+( +b-2)(
+b-2)(  +b-2
+b-2 b)
b)
解:原式=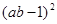 +
+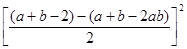 -
-
=( b-1)2+(
b-1)2+( +b-
+b- b-1)2-(
b-1)2-( b-1)2=(
b-1)2=( -1)(b-1)2=(
-1)(b-1)2=( -1)2(b-1)2你能利用公式(或其他方法)解决下列问题吗?
-1)2(b-1)2你能利用公式(或其他方法)解决下列问题吗?
已知各实数 ,b,c满足
,b,c满足 b=c2+9且
b=c2+9且 =6-b,求证:
=6-b,求证: ="b"
="b"
阅读并解答下列问题:我们熟悉两个乘法公式:①( +b)2=
+b)2= 2+2
2+2 b+b2;②(
b+b2;②( -b)2=
-b)2= 2-2
2-2 b+b2.现将这两个公式变形,可得到一个新的公式③:
b+b2.现将这两个公式变形,可得到一个新的公式③: b=(
b=(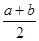 )2-(
)2-(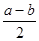 )2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
)2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
例如:因式分解:( b-1)2+(
b-1)2+( +b-2)(
+b-2)(  +b-2
+b-2 b)
b)
解:原式=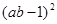 +
+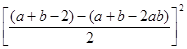 -
-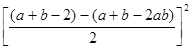
=( b-1)2+(
b-1)2+( +b-
+b- b-1)2-(
b-1)2-( b-1)2=(
b-1)2=( -1)(b-1)2=(
-1)(b-1)2=( -1)2(b-1)2你能利用公式(或其他方法)解决下列问题吗?
-1)2(b-1)2你能利用公式(或其他方法)解决下列问题吗?
已知各实数 ,b,c满足
,b,c满足 b=c2+9且
b=c2+9且 =6-b,求证:
=6-b,求证: ="b"
="b"
(1)请你任意写出3个正的真分数:____,___,___,给每个分数的分子、分母同加一个相同正数得到三个新分数:____,____,____,
(2)比较原来每个分数与对应新分数的大小,可以得出下面的结论:
一个真分数是![]() (
(![]() ,
,![]() 均为正数),给其分子分母同加一个正数
均为正数),给其分子分母同加一个正数![]() ,得
,得![]() ,则两个分数的大小关系是
,则两个分数的大小关系是![]() ________
________![]() .
.
(3)请你用文字叙述(2)中结论的含义:______________________ ___________________
(4)请你用图形的面积或其他方法说明这个结论的正确性。
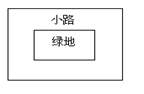
(5)解决问题:如图所示,有一个长宽不等的长方形绿地,现给绿地四周铺一条宽相等的小路,问原来的长方形绿地与现在铺过小路后的长方形绿地是否相似?为什么?
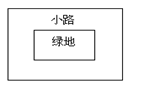
(6)这个结论可以解释生活中的许多现象,解决许多生活与数学中的问题,请你再提出一个类似的数学问题,或举出一个生活中与此结论相关的例子.
 (
( ,
, 均为正数),给其分子分母同加一个正数
均为正数),给其分子分母同加一个正数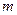 ,得
,得 ,则两个分数的大小关系是
,则两个分数的大小关系是 ________
________ .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com