
题目列表(包括答案和解析)
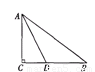
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式.



如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么点D到直线AB的距离是 ( )
A.3 cm B.5 cm C.6 cm D.8 cm
| A.8 | B.24 | C.12 | D.16 |
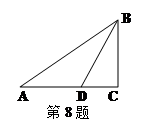
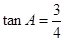 ,则AC 的长是 ▲ cm.
,则AC 的长是 ▲ cm.(6分)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,根据下面的条件解这个三角形:
(1)a=4,b=4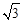 ; (2)a=3
; (2)a=3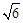 ,∠A=45°
,∠A=45°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com