
题目列表(包括答案和解析)
(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
 (m为常数)图象的一支.
(m为常数)图象的一支.
 图象在第一象限的交点为A(2,n),
图象在第一象限的交点为A(2,n),.(本小题满分12分)
如图,AD为△ABC的中线,BE为△ABD的中线。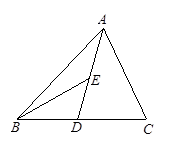
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
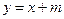 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在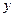 轴上.
轴上.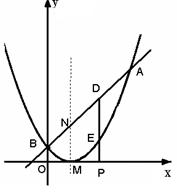
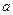 ,0) 是
,0) 是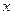 轴上的一个动点,过P作
轴上的一个动点,过P作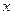 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.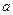 < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;(本小题满分12分)
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA="16" cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用含t的式子表示△OPQ的面积S;
(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;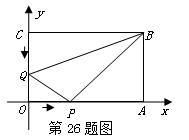 (3)当△OPQ∽△ABP时,抛物线y=
(3)当△OPQ∽△ABP时,抛物线y=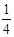 x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式;
(4)在(3)的条件下,过线段BP上一动点M作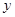 轴的平
轴的平
行线交抛物线于N,求线段MN的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com