练习册

  • 练习册
  • 试题
    线段与圆 例2. 已知⊙O的半径为5cm.梯形ABCD内接于⊙O.AD∥BC.且AD=6cm.BC=8cm.求梯形ABCD的面积. 分析 要求梯形面积需知梯形的高.由圆的对称性.知梯形的上.下底的位置可在圆心的同侧或异侧.所以应分两种情况分别求出上.下底之间的距离.然后求出面积. 解 (1)当AD和BC在圆心异侧时.如图4. 图4 过O作OE⊥AD.OF⊥BC.垂足分别为E.F. 因为 AD∥BC. 所以 E.O.F三点共线. 所以 AD和BC的距离 . 此时.. (2)当AD和BC在圆心同侧时.如图5.得 图5 此时. . 所以梯形ABCD的面积为7cm2或49cm2. 【查看更多】

     

    题目列表(包括答案和解析)

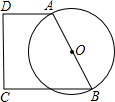
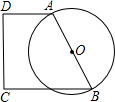    精英家教网如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以腰AB为直径作圆，已知AB=10，AD=M，BC=M+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则M的取值范围是（　　）
    A、0≤M≤3B、0＜M＜3C、0＜M≤3D、3＜M＜10

    查看答案和解析>>

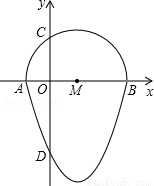
    如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2-2x-3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为　

     

     

    查看答案和解析>>

    如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以腰AB为直径作圆，已知AB=10，AD=M，BC=M+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则M的取值范围是（　　）
    A．0≤M≤3B．0＜M＜3C．0＜M≤3D．3＜M＜10
    精英家教网

    查看答案和解析>>

    定义：P，Q分别是两条线段a和b上任意一点，线段PQ长度的最小值叫做线段与线段的距离，已知O（0，0），A（4，0），B（m，n），C（m+4，n）是平面直角系中四点。
    （1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是_____，
    当m=5，n=2时，如图2，线段BC与线段OA的距离（即线段AB的长）为______；
    （2）如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式；
    （3）当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M。
    ①求出点M随线段BC运动所围成的封闭图形的周长；
    ②点D的坐标为（0，2），m≥0，n≥0，作MH⊥x轴，垂足为H，是否存在m的值，使以A，M，H为顶点的三角形与△AOD相似，若存在，求出m的值，若不存在，请说明理由。

    查看答案和解析>>

    如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点(点P与点C不重合)，连结BP. 将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P,连结AA1，射线AA1分别交射线PB、射线B1B于点E、F.

    　　 （1） 如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在 ▲ 关系（填“相似”或“全等”），并说明理由；

    （2）如图2，设∠ABP=β . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；

    （3）如图3，当α=60°时，点E、F与点B重合. 已知AB=4，设DP=x，△A1BB1的面积为S，求S关于x的函数关系式.

    查看答案和解析>>


    同步练习册答案