
题目列表(包括答案和解析)
|
|
|
|
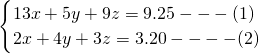 ;
;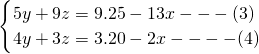 .
.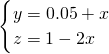 .
.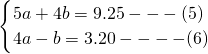 .
.
解:(1)△AFB∽△FEC.
证明:由题意得:∠AFE=∠D=90° 又∠B=∠C=90°
∴∠BAF+∠AFB=90° , ∠EFC+∠AFB=90°
∴∠BAF=∠EFC ∴ AFB∽△FEC
(2)设EC=3x,FC=4x,则有DE=EF=5x ,∴AB=CD=3x+ 5x=8x
由△AFB∽△FEC得:![]() 即:
即:![]() =
=![]() ∴BF=6x ∴BC=BF-CF=6x+ 4x= 10x
∴BF=6x ∴BC=BF-CF=6x+ 4x= 10x
∴在Rt△ADE中,AD=BC=10x,AE=![]() ,则有
,则有![]()
解得![]() (
(![]() 舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
阅读下列解题过程,借鉴其中一种方法解答后面给出的试题:
问题:某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元.
分析:设买鸡蛋,鸭蛋、鹅蛋各一个分别需x、y、z元,则需要求x+y+z的值.由题意,知![]() ;
;
视![]() 为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
解法1:视![]() 为常数,依题意得
为常数,依题意得![]()
解这个关于y、z的二元一次方程组得![]()
于是![]() .
.
评注:也可以视z为常数,将上述方程组看成是关于![]() 、
、![]() 的二元一次方程组,解答方法同上,你不妨试试.
的二元一次方程组,解答方法同上,你不妨试试.
分析:视![]() 为整体,由(1)、(2)恒等变形得
为整体,由(1)、(2)恒等变形得
![]() ,
,
![]() .
.
解法2:设![]() ,
,![]() ,代入(1)、(2)可以得到如下关于
,代入(1)、(2)可以得到如下关于![]() 、
、![]() 的二元一次方
的二元一次方
程组![]()
由⑤+4×⑥,得![]() ,
,![]() .
.
评注:运用整体的思想方法指导解题.视![]() ,
,![]() 为整体,令
为整体,令![]() ,
,![]() ,代人①、②将原方程组转化为关于
,代人①、②将原方程组转化为关于![]() 、
、![]() 的二元一次方程组从而获解.
的二元一次方程组从而获解.
请你运用以上介绍的任意一种方法解答如下数学竞赛试题:
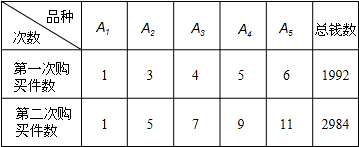
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表:
|
次数 | A1 | A2 | A3 | A4 | A5 | 总钱数 |
| 第一次购 买件数 | l | 3 | 4 | 5 | 6 | 1992 |
| 第二次购 买件数 | l | 5 | 7 | 9 | 11 | 2984 |
那么,购买每种教学用具各一件共需多少元?
阅读以下材料并完成后面的问题:
将直线y=2x-3向右平移3个单位长度,再向上平移1个单位长度,求平移后的直线的表达式.
解:在直线y=2x-3上任取两点A(1,-1)和B(0,-3).
由题意,知点A(1,-1)向右平移3个单位长度得到点![]() (4,-1),再向上平移1个单位长度得点
(4,-1),再向上平移1个单位长度得点![]() (4,0);点B(0,-3)向右平移3个单位长度得到
(4,0);点B(0,-3)向右平移3个单位长度得到![]() (3,-3),再向上平移1个单位长度得到点
(3,-3),再向上平移1个单位长度得到点![]() (3,-2).设平移后的直线的表达式为y=kx+b,由点
(3,-2).设平移后的直线的表达式为y=kx+b,由点![]() (4,0)、
(4,0)、![]() (3,-2)在该直线上,得0=4k+b,-2=3k+b.解得k=2,b=-8.所以平移后的直线的表达式为y=2x-8.
(3,-2)在该直线上,得0=4k+b,-2=3k+b.解得k=2,b=-8.所以平移后的直线的表达式为y=2x-8.
根据上面材料解答下面的问题:
将二次函数y=-x2+2x+3的图象向左平移1个单位长度,再向下平移2个单位长度,求平移后的抛物线的表达式(平移后抛物线的形状不变).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com