24.（本小题满分14分）

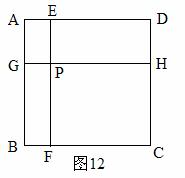
如图12，边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形，EF与GH交于点P。

（1）若AG=AE，证明：AF=AH；

（2）若∠FAH=45°，证明：AG+AE=FH；

（3）若RtΔGBF的周长为1，求矩形EPHD的面积。

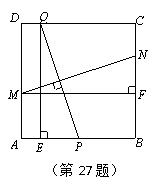
（本题满分12分）如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ＝t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．

（1）当t≠1时，求证：△PEQ≌△NFM；

（2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

 

 

 

 

 

 

 

 

 

 

 

（本题满分12分）如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ＝t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．

（1）当t≠1时，求证：△PEQ≌△NFM；

（2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

 

 

 

 

 

 

 

 

 

 

 

（本题满分12分）
【小题1】（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，
AB=BC．∴∠NMC=180°—∠AMN­—∠AMB=180°—∠B—∠AMB=∠MAB
=∠MAE．
（下面请你完成余下的证明过程）

【小题2】（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

【小题3】（3）若将（1）中的“正方形ABCD”改为“正边形ABCD…X”，请你作出猜想：当∠AMN=        °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

（本题满分12分）如图，已知直线交坐标轴于A、B点，以线段AB为边向上作正方形ABCD，过点A、D、C的抛物线与直线的另一个交点为E.

【小题1】（1）填空：点A的坐标为           ，点B的坐标为           ，AB的长为           ．
【小题2】（2）求点C、D的坐标
【小题3】（3）求抛物线的解析式
【小题4】（4）若抛物线与正方形沿射线AB下滑，直至点C落在轴上时停止，则抛物线上C、E两点间的抛物线所扫过的面积为           ．