
题目列表(包括答案和解析)
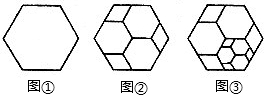
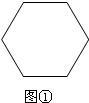

 将图①所示的正六边形进行分割得到图②,再将图②里的三个小正六边形的其中之一按同样的方式进行分割得到图③,接着再将图③中最小的三个正六边形的其中之一按同样的方式进行分割…,则第n 图形中共有
将图①所示的正六边形进行分割得到图②,再将图②里的三个小正六边形的其中之一按同样的方式进行分割得到图③,接着再将图③中最小的三个正六边形的其中之一按同样的方式进行分割…,则第n 图形中共有
|
|
|
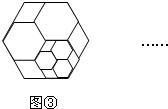
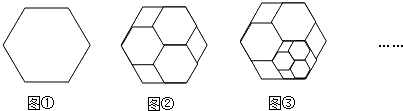
 16、将图①所示的正六边形进行进行分割得到图②,再将图②中最小的某一个正六边形按同样的方式进行分割得到图③,再将图③中最小的某一个正六边形按同样的方式进行分割…,则第n个图形中,共有
16、将图①所示的正六边形进行进行分割得到图②,再将图②中最小的某一个正六边形按同样的方式进行分割得到图③,再将图③中最小的某一个正六边形按同样的方式进行分割…,则第n个图形中,共有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com