
题目列表(包括答案和解析)
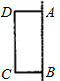 如图,以矩形ABCD的边AB所在直线为轴将其旋转一周,所形成的几何体的俯视图是( )
如图,以矩形ABCD的边AB所在直线为轴将其旋转一周,所形成的几何体的俯视图是( )如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线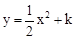 与扇形OAB的边界总有两个公共点,则实数k的取值范围是
与扇形OAB的边界总有两个公共点,则实数k的取值范围是
.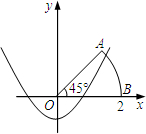
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线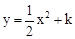 与扇形OAB的边界总有两个公共点,则实数k的取值范围是
与扇形OAB的边界总有两个公共点,则实数k的取值范围是
.
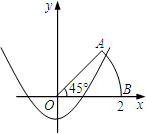
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=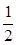 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .

如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com