
题目列表(包括答案和解析)
下面是小明化简分式的过程,请仔细阅读,并解答所提出的问题。
![]() ………………………第一步
………………………第一步
=2(x-2)-x-6……………………………………………………………第二步
=2x-4-x+6…………………………………………………………………第三步
=x+2………………………………………………………………………第四步
小明的解法从第 (2分)步开始出现错误,正确的化简结果是 。(3分)
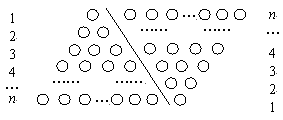
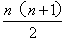 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=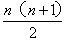 。
。
(1)计算: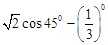 .
.
(2)下面是小明化简分式的过程,请仔细阅读,并解答所提出的问题。
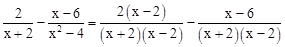 ………………………第一步
………………………第一步
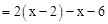 …………………………………………………………第二步
…………………………………………………………第二步
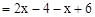 ……………………………………………………………第三步
……………………………………………………………第三步
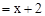 ………………………………………………………………………第四步
………………………………………………………………………第四步
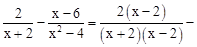 小明的解法从第 步开始出现错误,正确的化简结果是 。
小明的解法从第 步开始出现错误,正确的化简结果是 。
 .
. ………………………第一步
………………………第一步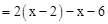 …………………………………………………………第二步
…………………………………………………………第二步 ……………………………………………………………第三步
……………………………………………………………第三步 ………………………………………………………………………第四步
………………………………………………………………………第四步 小明的解法从第 步开始出现错误,正确的化简结果是 。
小明的解法从第 步开始出现错误,正确的化简结果是 。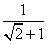 =
=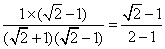 =
=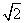 -1;
-1;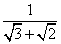 =
=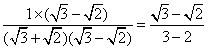 =
=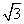 -
- ,
, =
=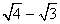 ,…
,…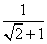 +
+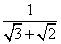 +
+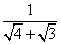 +…+
+…+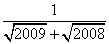 )(
)(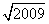 +1)的值。
+1)的值。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com