题目列表(包括答案和解析)
如图，已知：如图(1)，AB是⊙O的直径，P是AB上的一点(与A、B不重合)．QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：
证明：连结OC．
∵OA＝OC，∴∠A＝∠1．
∵CD切⊙O于C点，
∴∠OCD＝90°，
∴∠1＋∠2＝90°，
∴∠A＋∠2＝90°．
在Rt△QPA中，∠QPA＝90°，
∴∠A＋∠Q＝90°，
∴∠2＝∠Q．∴DQ＝DC．
即△CDQ是等腰三角形．
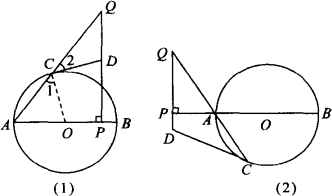
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图(2)所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
如图，AB是⊙
的直径，P是AB上一点(与点A，B不重合)，QP⊥AB，垂足为P点，直线QA交⊙于C点，过点C作⊙的切线交直线QP于点D．则△CDQ是等腰三角形．对上述命题证明如下：
证明：连接OC．
∵OA=OC，∴∠A=∠1．
∵CD切⊙于C点，
∴∠OCD=90°，∴∠1+∠2=90°，∴∠A+∠2=90°．
在Rt△QPA中，∠QPA=90°，
∴∠A+∠Q=90°，∴∠2=∠Q，∴DQ=DC．
即△CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变．
如图所示，结论“△CDQ是等腰三角形”还成立吗?若成立，请给予证明；若不成立，请说明理由．
已知：如图所示，AB是⊙O的直径，P是AB上的一点(与A、B不重合)，QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：
证明：连接OC．
∵OA=OC，
∴∠A＝∠1．
∵CD切⊙O于C点，
∴∠OCD＝90°．
∴∠1＋∠2＝90°．
∴∠A＋∠2=90°．
在Rt△QPA中，∠QPA＝90°，
∴∠A＋∠Q=90°．
∴∠2=∠Q．∴DQ＝DC．
即△CDQ是等腰三角形
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，结论“△CDQ是等腰三角形”还成立吗?若成立，请给予证明；若不成立，请说明理由．
阅读材料并解答问题：
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，…，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n(n≥3)边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．(结果可用三角函数表示)
如图①，当n＝3时，设AB切圆O于点C，连结OC，OA，OB，
∴OC⊥AB，OA＝OB，∴∠AOC＝
AOB，AB＝2BC．
在Rt△AOC中，
，OC＝r，
∴AC＝r·tan60°，AB＝2r·tan60°，
∴S△OAB＝
·r·2rtan60°＝r2tan60°，
∴S正三角形＝3S△OAB＝3r2·tan60°．
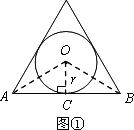
(1)如图②，当n＝4时，仿照(1)中的方法和过程可求得：S正四边形＝________；
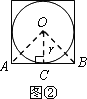
(2)如图③，当n＝5时，仿照(1)中的方法和过程求S正五边形；
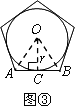
(3)如图④，根据以上探索过程，请直接写出S正n边形________．
(2005 福州)已知：如图所示，AB是⊙O的直径，P是AB上的一点(与A、B不重合)，QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形，对上述命题证明如下：
证明 连接OC．∵OA=OC=OC，∴∠A==∠1．
∵CD切⊙O于C点，∴∠OCD=90=90°，
∴∠1＋∠2=90°，∴∠A＋∠2=90°，
在Rt△QPA中，∠QPA=90=90°，
∴∠A＋∠Q=90=90°，∴∠2=∠Q．∴DQ=DC=DC．
即△CDQ是等腰三角形．
问题 对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com