(本小题满分6分) 

解不等式组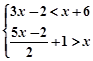：，并把解集在数轴上表示出来.

(本小题满分8分)

为减少环境污染，自2008年6月1日起，全国的商品零售场所开始实行“塑料购物袋有偿使用制度”（以下简称“限塑令”）．某班同学于6月上旬的一天，在某超市门口采用问卷调查的方式，随机调查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以下是根据100位顾客的100份有效答卷画出的统计图表的一部分：

“限塑令”实施后，塑料购物袋使用后的处理方式统计表

请你根据以上信息解答下列问题：

（1）补全图1，“限塑令”实施前，如果每天约有2 000人次到该超市购物．根据这100位顾客平均一次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少个塑料购物袋？

（2）补全图2，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用后怎样处理，能对环境保护带来积极的影响．

(本小题满分14分)平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别为(0，3)、(，0)，将此平行四边形绕点0顺时针旋转90°，得到平行四边形。

(1)若抛物线过点C，A，，求此抛物线的解析式；

(2)求平行四边形ABOC和平行四边形重叠部分△的周长；

(3)点M是第一象限内抛物线上的一动点，间：点M在何处时△的面积最大?最大面积是多少?并求出此时点M的坐标。

(本小题满分12分)

在平面直角坐标系xOy中，抛物线的解析式是y =+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.

 (1) 写出点M的坐标；

 (2) 当四边形CMQP是以MQ，PC为腰的梯形时.

① 求t关于x的函数解析式和自变量x的取值范围；

② 当梯形CMQP的两底的长度之比为1：2时，求t的值.

(本小题满分7分)

⑴解不等式组：

⑵如图所示，在梯形ABCD中，BC∥AD，AB=DC，点M是AD的中点．

求证：BM=CM．