注意：为了使学生更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求，进行解答．
在2008年春运期间，我国南方出现大范围冰雪灾害，导致某地电路断电．该地供电局组织电工进行抢修．供电局距离抢修工地15千米．抢修车装载着所需材料先从供电局出发，15分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的1.5倍，求这两种车的速度．
解题方案：设抢修车的速度为x千米/时，
（Ⅰ）用含x的代数式表示：
吉普车的速度是米/小时，抢修车到达抢修工地需要小时，吉普车到达抢修工地需要小时．
（Ⅱ）根据题意，列出相应方程；
（Ⅲ）解这个方程，得；
（Ⅳ）检验：；
（Ⅴ）答：抢修车和吉普车两车的速度分别是千米/小时（用数字作答）．

注意：为了使同学们更好地解答本题，下面提供了一种解题思路，你可以依照这个思路填空，并完成本题解答的全过程．如果你选用其他的解题方案，此时，不必填空，只需按照解答题的一般要求，进行解答即可．
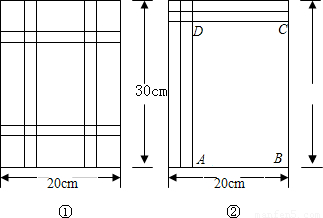
如图①，要设计一幅宽20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2：3，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？
分析：由横、竖彩条的宽度比为2：3，可设每个横彩条的宽为2x，则每个竖彩条的宽为3x．为更好地寻找题目中的等量关系，将横、竖彩条分别集中，原问题转化为如图②的情况，得到矩形ABCD．
结合以上分析完成填空：如图②，用含x的代数式表示：
AB=______cm；
AD=______cm；
矩形ABCD的面积为______ cm²．
列出方程并完成本题解答．