
题目列表(包括答案和解析)
将Rt△ABC沿斜边AB向右平移5 cm,得到Rt△DEF.已知AB=10 cm,BC=8 cm,求图中阴影部分三角形的面积.
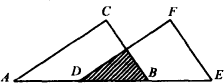
将
Rt△ABC沿斜边AB向右平移5 cm,得到Rt△DEF.已知AB=10 cm,BC=8 cm,求图中DEF的周长和DB的长.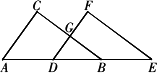
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | 2 |

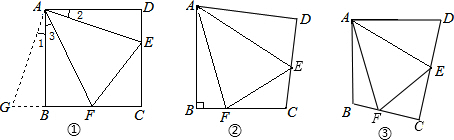
如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.

(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;
(2)在图1中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系;
(3)如图2,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF= ∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com