
题目列表(包括答案和解析)
(1)等腰梯形的性质有:①两底________,两腰________;②等腰梯形在同一个________相等;③等腰梯形的两条________相等;
(2)等腰梯形的判定有:①________的梯形是等腰梯形;②________的梯形是等腰梯形.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
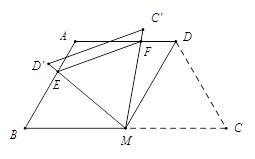
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
【解析】此题考核等边三角形的判定,旋转的性质
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
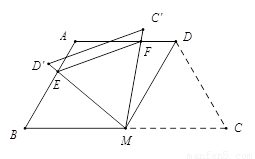
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
【解析】此题考核等边三角形的判定,旋转的性质
 来逐步认识四边形;
来逐步认识四边形;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com