
题目列表(包括答案和解析)
解答题
已知如图,AO⊥BC,DO⊥OE.
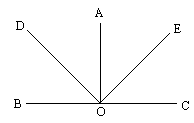
(1)不添加其它条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE=![]() ,求∠AOD的度数.
,求∠AOD的度数.
解答题
已知如图,AB是![]() O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,求证EC=DF.
O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,求证EC=DF.

解答题:
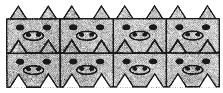
观察如图所示的图案,它可以看做是由什么“基本图案”通过平移得到的?
解答题
(1)画出图中甲、乙的立体图形的三视图.
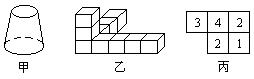
(2)如图丙所示是由几个小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.请画出这个几何体的主视图和左视图.
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com