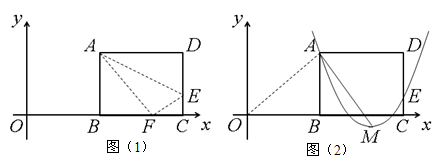
（本题满分12分）如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折

叠边AD,使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m,0），其中m＞0.

1.（1）求点E、F的坐标（用含m的式子表示）；

2.（2）连接OA，若△OAF是等腰三角形，求m的值；

3.（3）如图（2），设抛物线经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值.

（本题满分12分）如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折
叠边AD,使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m,0），其中m＞0.

【小题1】（1）求点E、F的坐标（用含m的式子表示）；
【小题2】（2）连接OA，若△OAF是等腰三角形，求m的值；
【小题3】（3）如图（2），设抛物线经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值.

（本题满分12分）如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折

叠边AD,使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m,0），其中m＞0.

1.（1）求点E、F的坐标（用含m的式子表示）；

2.（2）连接OA，若△OAF是等腰三角形，求m的值；

3.（3）如图（2），设抛物线经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值.

（本小题满分10分）

    学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

根据上述对角的正对定义，解下列问题：

（1）sad 的值为（   ）A.       B.1  C.      D.2

（2）对于，∠A的正对值sad A的取值范围是        .

（3）已知，其中为锐角，试求sad的值.