
题目列表(包括答案和解析)
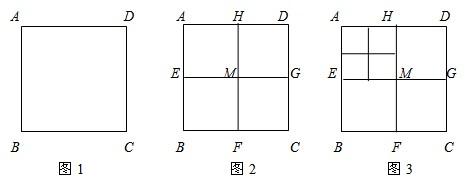
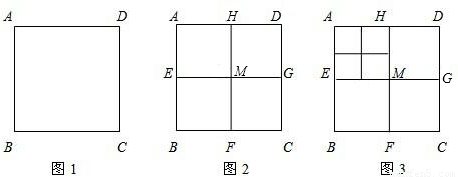
将正方形ABCD(如下图1)作如下划分:
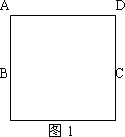
第1次划分:分别联结正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
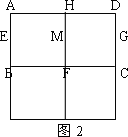
第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有________个正方形;
若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有________个正方形;
继续划分下去,能否将正方形ABCD划分成有2011个正方形的图形?需说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com