
题目列表(包括答案和解析)
如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角![]() ,量得树干倾斜角
,量得树干倾斜角![]() ,大树被折断部分和坡面所成的角
,大树被折断部分和坡面所成的角![]() .
.

(1)求![]() 的度数;
的度数;
(2)求这棵大树折断前的高度?(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() ).
).
【解析】(1)通过延长BA交EF于一点M,则∠CAD=180°-∠BAC-∠EAM即可求得;
(2)作AH⊥CD于H点,作CG⊥AE于G点,先求得CD的长,然后再求得AC的长,最后求得这棵大树折断前的高度
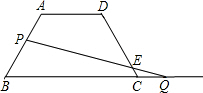
如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角 ,量得树干倾斜角
,量得树干倾斜角 ,大树被折断部分和坡面所成的角
,大树被折断部分和坡面所成的角 .
.

(1)求 的度数;
的度数;
(2)求这棵大树折断前的高度?(结果精确到个位,参考数据: ,
, ,
,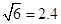 ).
).
【解析】(1)通过延长BA交EF于一点M,则∠CAD=180°-∠BAC-∠EAM即可求得;
(2)作AH⊥CD于H点,作CG⊥AE于G点,先求得CD的长,然后再求得AC的长,最后求得这棵大树折断前的高度
 发,点P沿射线AB、点Q沿BC的延长线均以1cm/s的速度作匀速直线运动.
发,点P沿射线AB、点Q沿BC的延长线均以1cm/s的速度作匀速直线运动.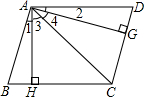 如图,过?ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G,且AH≠AG,AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4,则下列关系正确的是( )
如图,过?ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G,且AH≠AG,AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4,则下列关系正确的是( )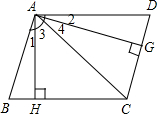 (2012•邗江区一模)如图,过平行四边形ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G,AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4,AH=5,AG=6,则下列关系正确的是( )
(2012•邗江区一模)如图,过平行四边形ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G,AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4,AH=5,AG=6,则下列关系正确的是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com