(本题满分7分)如图，已知在Rt△ABC，AB＝AC，∠BAC＝90°，过A的任一条直线AN，BD⊥AN于D，CE⊥AN于E。
⑴求证：DE＝BD－CE
⑵如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间存在等量关系吗？若存在，请证明你的结论？

(本题满分7分)如图，已知在Rt△ABC，AB＝AC，∠BAC＝90°，过A的任一条直线AN，BD⊥AN于D，CE⊥AN于E。

⑴求证：DE＝BD－CE

⑵如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间存在等量关系吗？若存在，请证明你的结论？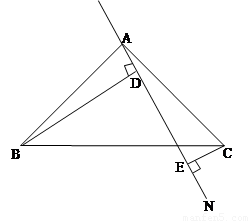

（本题满分10分）

如图，在正方形网格图中建立一直角 坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：

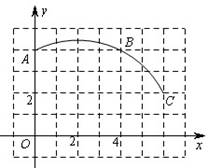
1.(1) 利用网格确定该圆弧所在圆的圆心D点的 位置（保留画图痕迹），则D点坐标为   ▲   ；

 2.(2) 连接AD、CD，则⊙D的半径为   ▲   (结果保留根号)，∠ADC的度数为   ▲    度；

3.(3)若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面的半径．(结果保留根号)

（本题满分12分）如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b

与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．

(1)OH的长度等于___________；k＝___________，b＝____________；

(2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶

点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜，写出探索过程．