
题目列表(包括答案和解析)
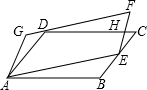 C上,CD与EF相交于点H,设△ABE、△ECH、△HFD、△DGA的面积分别为S1、S2、S3、S4,给出下列结论:
C上,CD与EF相交于点H,设△ABE、△ECH、△HFD、△DGA的面积分别为S1、S2、S3、S4,给出下列结论: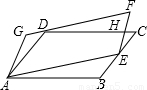

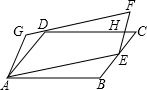 C上,CD与EF相交于点H,设△ABE、△ECH、△HFD、△DGA的面积分别为S1、S2、S3、S4,给出下列结论:
C上,CD与EF相交于点H,设△ABE、△ECH、△HFD、△DGA的面积分别为S1、S2、S3、S4,给出下列结论:Ð1=60°,Ð2=30°,GH^CD于点H.
解:∵ GH^CD(已知)∴ Ð2+Ð3=________(垂直定义)
∵ Ð2=30°(已知)∴ Ð3=90°-30°=60°
∵ Ð3=Ð4=60°(________)Ð1=60°(已知)
∴ Ð1=Ð4 ∴ AB∥________(________).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com