练习册

  • 练习册
  • 试题
    24．解:(1)设抛物线的解析式为y=kx2+a ∵点D(2a.2a)在抛物线上. 4a2k+a = 2a ∴k = ∴抛物线的解析式为y= x2+a (2)设抛物线上一点P(x.y).过P作PH⊥x轴.PG⊥y轴.在Rt△GDP中. 由勾股定理得:PD2=DG2+PG2=(y–2a)2+x2 =y2 – 4ay+4a2+x2 ∵y= x2+a ∴x2 = 4a ´ (y– a)= 4ay– 4a2 ∴PD 2= y2– 4ay+4a2 +4ay– 4a2= y2 =PH2 ∴PD = PH (3)过B点BE ⊥ x轴.AF⊥x轴. 由(2)的结论:BE=DB AF=DA ∵DA=2DB ∴AF=2BE ∴AO = 2BO ∴B是OA的中点. ∴C是OD的中点. 连结BC ∴BC= = = BE = DB 过B作BR⊥y轴. ∵BR⊥CD ∴CR=DR.OR= a + = . ∴B点的纵坐标是.又点B在抛物线上. ∴ = x2+a ∴x2 =2a2 ∵x>0 ∴x = a ∴B (a. ) AO = 2OB. ∴S△ABD=S△OBD = 4 所以.´2a´a= 4 ∴a2= 4 ∵a>0 ∴a = 2 【查看更多】

     

    题目列表(包括答案和解析)

    22、如图，某灌溉设备的喷头B高出地面1.25m，喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m．试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式．
    小明在解答下图所示的问题时，写下了如下解答过程：

    ①以水流的最高点为原点，过原点的水平线为横轴，过原点的铅垂线为纵轴建立如图所示的平面直角坐标系；
    ②设抛物线的解析式为y=ax2；
    ③则B点的坐标为（-1，-1）；
    ④代入y=ax2，得-1=a•1，所以a=-1
    ⑤所以y=-x2
    问：（1）小明的解答过程是否正确，若不正确，请你加以改正；
    （2）喷出的水流能否浇灌到地面上距离A点3.5m的庄稼上（图上庄稼在A点的右侧，庄稼的高度不计），若不能请你在上图所示的坐标系中将喷头B上下或左右平移，问至少要平移多少距离才能浇灌到地面的庄稼，并求出此时喷出的抛物线形水流的函数解析式．

    查看答案和解析>>

    如图，某灌溉设备的喷头B高出地面1.25m，喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m．试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式．
    小明在解答下图所示的问题时，写下了如下解答过程：

    ①以水流的最高点为原点，过原点的水平线为横轴，过原点的铅垂线为纵轴建立如图所示的平面直角坐标系；
    ②设抛物线的解析式为y=ax2；
    ③则B点的坐标为（-1，-1）；
    ④代入y=ax2，得-1=a•1，所以a=-1
    ⑤所以y=-x2
    问：（1）小明的解答过程是否正确，若不正确，请你加以改正；
    （2）喷出的水流能否浇灌到地面上距离A点3.5m的庄稼上（图上庄稼在A点的右侧，庄稼的高度不计），若不能请你在上图所示的坐标系中将喷头B上下或左右平移，问至少要平移多少距离才能浇灌到地面的庄稼，并求出此时喷出的抛物线形水流的函数解析式．

    查看答案和解析>>

    如图，某灌溉设备的喷头B高出地面1.25m，喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m．试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式．
    小明在解答下图所示的问题时，写下了如下解答过程：

    ①以水流的最高点为原点，过原点的水平线为横轴，过原点的铅垂线为纵轴建立如图所示的平面直角坐标系；
    ②设抛物线的解析式为y=ax2；
    ③则B点的坐标为（-1，-1）；
    ④代入y=ax2，得-1=a•1，所以a=-1
    ⑤所以y=-x2
    问：（1）小明的解答过程是否正确，若不正确，请你加以改正；
    （2）喷出的水流能否浇灌到地面上距离A点3.5m的庄稼上（图上庄稼在A点的右侧，庄稼的高度不计），若不能请你在上图所示的坐标系中将喷头B上下或左右平移，问至少要平移多少距离才能浇灌到地面的庄稼，并求出此时喷出的抛物线形水流的函数解析式．

    查看答案和解析>>

    如图，某灌溉设备的喷头B高出地面1.25m，喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m．试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式．
    小明在解答下图所示的问题时，写下了如下解答过程：

    ①以水流的最高点为原点，过原点的水平线为横轴，过原点的铅垂线为纵轴建立如图所示的平面直角坐标系；
    ②设抛物线的解析式为y=ax2；
    ③则B点的坐标为（-1，-1）；
    ④代入y=ax2，得-1=a•1，所以a=-1
    ⑤所以y=-x2
    问：（1）小明的解答过程是否正确，若不正确，请你加以改正；
    （2）喷出的水流能否浇灌到地面上距离A点3.5m的庄稼上（图上庄稼在A点的右侧，庄稼的高度不计），若不能请你在上图所示的坐标系中将喷头B上下或左右平移，问至少要平移多少距离才能浇灌到地面的庄稼，并求出此时喷出的抛物线形水流的函数解析式．

    查看答案和解析>>

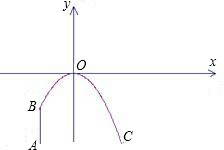
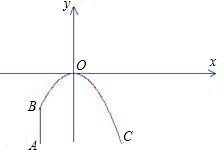
    目前国内最大跨径的钢管混凝土拱桥——永和大桥是南宁市又一标志性建筑，其中拱形图形为抛物线的一部分，如图．在正常情况下，位于水面上的桥拱跨度为350m，拱高为85m．

    (1)在如图所示的直角坐标系中，设抛物线的解析式为y＝ax2＋b．请你根据上述数据求出a、b的值，并写出抛物线的解析式(不要求写自变量的取值范围，a、b的值保留两个有效数字)．

    (2)7月份汛期将要来临，当邕江水位上涨后，位于水面上的桥拱跨度将会减小．当水位上涨4m时，位于水面上的桥拱跨度有多大？(结果保留整数)

    查看答案和解析>>


    同步练习册答案