
题目列表(包括答案和解析)


(2011•滨州)根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论.
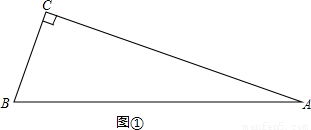
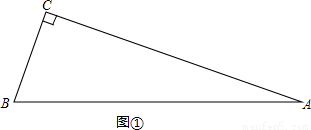
(1)如图①△ABC中,∠C=90°,∠A=24°
①作图:
②猜想:
③验证:
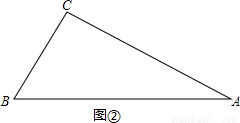
(2)如图②△ABC中,∠C=84°,∠A=24°.
①作图:
②猜想:
③验证:



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com