练习册

  • 练习册
  • 试题
    图1是一个边长为1的等边三角形和一个菱形的组合图形.菱形边长为等边三角形边长的一半.以此为基本单位.可以拼成一个形状相同但尺寸更大的图形.依此规律继续拼下去.-.则第n个图形的周长是( ) A.2n B.4n C.2n+1 D.2n+2 考点:规律型:图形的变化类,等边三角形的性质,菱形的性质. 专题:规律型. 分析:从图1到图3.周长分别为4.8.16.由此即可得到通式.利用通式即可求解． 解答:解:下面是各图的周长: 图1中周长为4, 图2周长为8, 图3周长为16, 所以第n个图形周长为2n+1． 故选C． 点评:本题考查了图形的变化规律.首先从图1到图3可得到规律.然后利用规律得到一般结论解决问题． 【查看更多】

     

    题目列表(包括答案和解析)

    （2013•福州质检）如图，边长为6的等边三角形ABC中，E是对称轴AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E运动过程中，DF的最小值是
    1.5
    1.5
    ．

    查看答案和解析>>

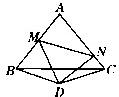    29、如图，△ABC是边长为l的等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB于M，交AC于N，连接MN，形成一个三角形，
    求证：△AMN的周长等于2．

    查看答案和解析>>

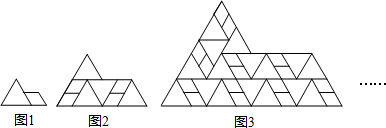    图1是一个边长为2的等边三角形和一个四边均长为1的四边形的组合图形，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第1个图形的周长是
    8
    8
    ；第4个图形的周长是
    64
    64
    ．

    查看答案和解析>>

    如图，由于水资源缺乏，B、C两地不得不从黄河上的扬水站A引水，这就需要A、B、C之间铺设地下输水管道，有人设计了三种铺设方案：如图①②③，图中实线表示管道铺设线路，在图②中，AD垂直BC于D；在图③中，OA=OB=OC．为减少渗漏，节约水资源，并降低工程造价，铺设线路应尽量缩短，已知△ABC恰好是一个边长为a的等边三角形，那么通过计算，你认为最好的铺设方案是方案
     
    ．
    精英家教网

    查看答案和解析>>

    如图，边长为2a的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（　　）
    A、
    		3
    a
    B、a
    C、
    		3
    2
    a
    D、
    1
    2
    a

    查看答案和解析>>


    同步练习册答案