
题目列表(包括答案和解析)
图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正
方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱
形有13个;铺成4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共181个时,n的值为
( )
A.7 B.8 C.9 D.10

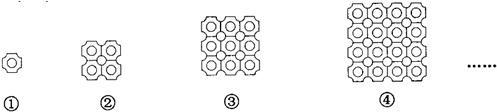
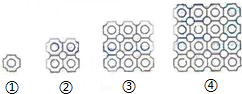
| A、100个 | B、101个 | C、181个 | D、221个 |
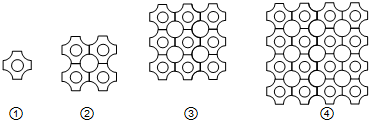
如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有 个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com