
题目列表(包括答案和解析)
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| (a+b)2-2ab |
| ab |
| 1 |
| q2 |
阅读与理解:
(1)先阅读下面的解题过程:
分解因式:
解:方法(1)原式



方法(2)原式



再请你参考上面一种解法,对多项式进 行因式分解;
行因式分解;
(2)阅读下面的解题过程:
已知 :,试求
:,试求 与
与 的值。
的值。
解:由已知得:
因此得到:
所以只有当 并且
并且 上式才能成立。
上式才能成立。
因而得: 并且
并且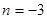
请你参考上面的解题方法解答下面的问题:
已知: ,试求
,试求 的值
的值
阅读与理解:
(1)先阅读下面的解题过程:
分解因式: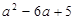
解:方法(1)原式



方法(2)原式



再请你参考上面一种解法,对多项式进 行因式分解;
行因式分解;
(2)阅读下面的解题过程:
已知 :,试求
:,试求 与
与 的值。
的值。
解:由已知得:
因此得到:
所以只有当 并且
并且 上式才能成立。
上式才能成立。
因而得: 并且
并且
请你参考上面的解题方法解答下面的问题:
已知: ,试求
,试求 的值
的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com