
题目列表(包括答案和解析)
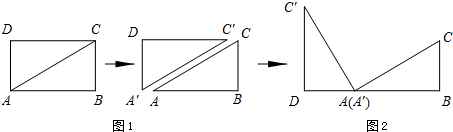




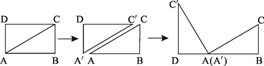
1.情境观察 将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 ,∠CAC′= °.

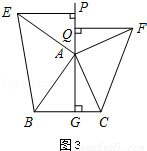
2.问题探究 如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.

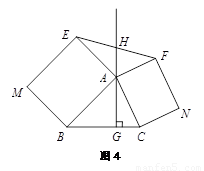
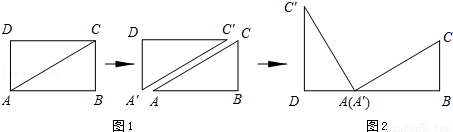
3.拓展延伸 如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由

1.情境观察 将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 ,∠CAC′= °.
2.问题探究 如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.

3.拓展延伸 如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由
情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 _________ ,∠CAC′= _________ °.
问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.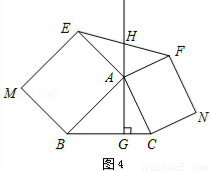
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com