
题目列表(包括答案和解析)
甲、乙两同学同时从400m环形跑道上的同一点出犮,同向而行.甲的速度为6m/s,乙的速度为4m/s.设经过x(单位:s)后,跑道上此两人间的较短部分的长度为y(单位:m).则y与x(0≤x≤300)之间的函数关系可用图象表示为( ).
(A)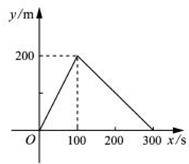 (B)
(B)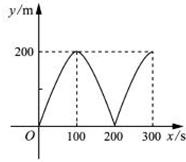
(C)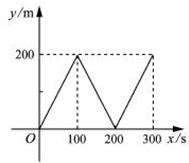 (D)
(D)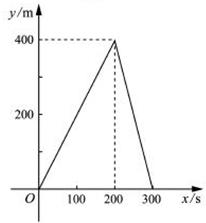
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com