练习册

  • 练习册
  • 试题
    如图.在▱ABCD中.E是BC的中点.且∠AEC=∠DCE.则下列结论不正确的是( ) A.S△AFD=2S△EFB B.BF=DF C.四边形AECD是等腰梯形 D.∠AEB=∠ADC 考点:平行四边形的性质,相似三角形的判定与性质. 分析:本题要综合分析.但主要依据都是平行四边形的性质． 解答:解:A.∵AD∥BC ∴△AFD∽△EFB ∴=== ∴S△AFD=2S△ABF.S△ABF=2S△EFB. 故S△AFD=4S△EFB, B.利用平行四边形的性质可知正确． C.由∠AEC=∠DCE可知正确． D.利用等腰三角形和平行的性质即可证明． 故选A． 点评:解决本题的关键是利用相似求得各对应线段的比例关系． 【查看更多】

     

    题目列表(包括答案和解析)

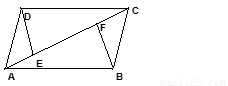
    如图，在▱ABCD中，点 E、F在对角线AC上，要使图中能够出现三对全等三角形，只需添加一个条件                   。（填写一种即可）

     

    查看答案和解析>>

    如图，在▱ABCD中，AC与BD相交于点O，则下列结论不一定成立的是（　　）

    A．BO=DO    B．CD=AB    C．∠BAD=∠BCD    D．AC=BD

     

    查看答案和解析>>

    如图，在▱ABCD中，对角线AC=21㎝，BE⊥AC，垂足为E，且BE=5㎝，AD=7㎝，则AD和BC之间的距离为               。

      

     

    查看答案和解析>>

    如图，在▱ABCD中，E为CD上一点，DE：CE=2：3，连接AE、BE、BD，且AE、BD交于点F，则S△DEF：S△EBF：S△ABF=______________.

     

     

    查看答案和解析>>

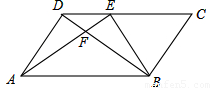
    如图，在▱ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF=　    　..

     

     

    查看答案和解析>>


    同步练习册答案