
题目列表(包括答案和解析)
如下图,为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离1千米的两个观察点C、D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为 (千米/分钟).


 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.(2006
上海,16)如图所示,平面中两条直线 和
和 相交于点O,对于平面上任意一点M,若p、q分别是M到直线
相交于点O,对于平面上任意一点M,若p、q分别是M到直线 和
和 的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;
的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;

①若
p=q=0,则“距离坐标”为(0,0)的点有且仅有1个.②若
pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个.③若
pq≠0,则“距离坐标”为(p,q)的点有且仅有4个.上述命题中,正确命题的个数是
[
]|
A .0 |
B .1 |
C .2 |
D .3 |
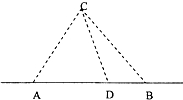 (2013•盐城二模)如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
(2013•盐城二模)如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com