
题目列表(包括答案和解析)
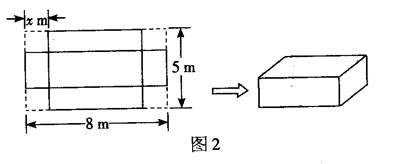
. (本小题满分12分)如图2所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?

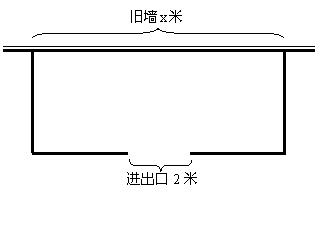
(本小题满分12分)围建一个面积为360平方米的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2米的进出口,如图所示,已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为![]() 米,工程总造价为
米,工程总造价为![]() (单位:元)。
(单位:元)。
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
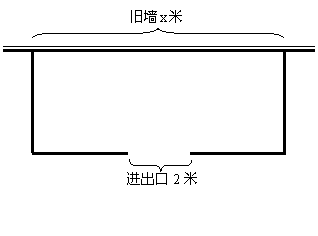
(本小题满分12分)围建一个面积为360平方米的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2米的进出口,如图所示,已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为![]() 米,工程总造价为
米,工程总造价为![]() (单位:元)。
(单位:元)。
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
(本小题满分12分)围建一个面积为360平方米的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2米的进出口,如图所示,已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为![]() 米,工程总造价为
米,工程总造价为![]() (单位:元)。
(单位:元)。
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com