
题目列表(包括答案和解析)
中学数学中存在许多关系,比如“相等关系”、“平行关系”等等,如果集合 中元素之间的一个关系“
中元素之间的一个关系“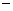 ”满足以下三个条件:
”满足以下三个条件:
(1)自反性:对于任意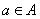 ,都有
,都有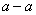 ;
;
(2)对称性:对于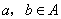 ,若
,若 ,则有
,则有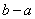 ;
;
(3)传递性:对于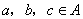 ,若
,若 ,
,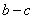 ,则有
,则有 则称“
则称“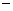 ”是集合
”是集合 的一个等价关系以下四种关系中不是等价关系的是 ( )
的一个等价关系以下四种关系中不是等价关系的是 ( )
A.数的相等 B.向量的共线 C.图形的相似 D.命题的充要条件
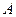 中元素之间的一个关系“
中元素之间的一个关系“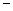 ”满足以下三个条件:
”满足以下三个条件: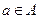 ,都有
,都有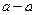 ;
;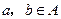 ,若
,若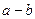 ,则有
,则有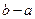 ;
;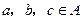 ,若
,若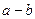 ,
,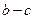 ,则有
,则有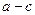 则称“
则称“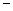 ”是集合
”是集合 的一个等价关系以下四种关系中不是等价关系的是 ( )
的一个等价关系以下四种关系中不是等价关系的是 ( )| A.数的相等 | B.向量的共线 | C.图形的相似 | D.命题的充要条件 |
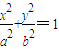 (a>b>0),其焦距为2c,若
(a>b>0),其焦距为2c,若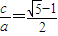 (≈0.618),则称椭圆C为“黄金椭圆”.
(≈0.618),则称椭圆C为“黄金椭圆”.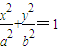 (a>b>0)中,a、b、c成等比数列.
(a>b>0)中,a、b、c成等比数列.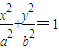 (a>b>0)的右焦点为F2(c,0),P为椭圆C上的任意一点.是否存在过点F2、P的直线l,使l与y轴的交点R满足
(a>b>0)的右焦点为F2(c,0),P为椭圆C上的任意一点.是否存在过点F2、P的直线l,使l与y轴的交点R满足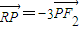 ?若存在,求直线l的斜率k;若不存在,请说明理由.
?若存在,求直线l的斜率k;若不存在,请说明理由.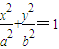 (a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),以A(-a,0)、B(a,0)、D(0,-b)、E(0,b)为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),以A(-a,0)、B(a,0)、D(0,-b)、E(0,b)为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.如图,已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4( +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.

(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
下列命题中,假命题为
A、存在四边相等的四边形不是正方形
B、z1,z2∈c,z1+z2为实数的充分必要条件是z1,z2互为共轭复数
C、若x,y∈CR,且x+y>2,则x,y至少有一个大于1
D、对于任意n∈N, +.
+. …+
…+ 都是偶数
都是偶数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com