
题目列表(包括答案和解析)
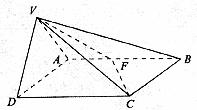
如图所示,△VAD是等边三角形,ABCD是矩形,![]() ,平面VAD⊥平面ABCD,F为AB中点。
,平面VAD⊥平面ABCD,F为AB中点。
(1)求VC与平面ABCD所成角的大小;
(2)当V到平面ABCD的距离为3时,求B到平面VFC的距离。
 如图所示,ABCD是边长为a的正方形,△ABP是以角B为直角的等腰三角形.
如图所示,ABCD是边长为a的正方形,△ABP是以角B为直角的等腰三角形.| 3 |
 如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.
如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB. (2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com