
题目列表(包括答案和解析)
已知向量的集合M={![]() |
|![]() =λ(1,0)+(1+λ2)(0,1),λ∈R},N={
=λ(1,0)+(1+λ2)(0,1),λ∈R},N={![]() |
|![]() =(1,6)+λ(2,4),λ∈R},则M∩N等于
=(1,6)+λ(2,4),λ∈R},则M∩N等于
A.{(-1,2)}
B.{(-1,2),(3,10)}
C.![]()
D.{(1,2),(-1,2)}
已知函数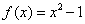 ,集合M=
,集合M=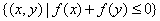 ,N=
,N=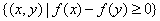 ,则集合
,则集合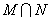 所表示的平面区域的面积是 .
所表示的平面区域的面积是 .
已知函数![]() ,集合M={(x,y)|f(x)+f(y)≤0},集合N={(x,y)|f(x)-f(y)≥0},则集合M∩N的面积为
,集合M={(x,y)|f(x)+f(y)≤0},集合N={(x,y)|f(x)-f(y)≥0},则集合M∩N的面积为
A.![]()
B.![]()
C.π
D.2π
已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知![]() ,求证
,求证![]() ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com