练习册

  • 练习册
  • 试题
    立足知识交汇处设计试题.全卷没有一道试题涉及的考点在两个或两个以下.具有一定的综合性.17题.融向量.三角.不等式于一体.再如理科第21题.将导数.数列.数学归纳法等融合.就是一个很好的明证.总之本套试卷较好地代表了高考的命题趋势和方向 测试总评 本套试题融入新课程新大纲的理念.贴近高考.试题立意新颖.选材不拘一格.从数学知识.思想方法.学科能力出发.多层次.多角度.多视点地考查学生的数学素养和学习的潜能.试题立足基础知识.突出对主干知识.如数列与函数.向量与三角.直线与圆锥曲线.导数与函数及数列.空间线面位置判断与证明及空间量的计算等知识的考查.突出对新教材新增内容如向量.导数.概率等新增知识的考查.这和新高考的要求相辉映.强化数学思想方法.对数学思想方法的考查贯穿于整个试卷之中.设置实际情景.突出对应用建模能力的考查.这也是呼应了近年来高考命题的重要思路.突出能力立意.在知识交汇处设计试题.注重通性通法.既注重了试题的创新.又尽量避免出现没有出偏题怪题.试题难度适中.总之.该套试题没有超越新考纲.全面综合地考查了学生的数学能力.试题有风格.有新意.对同学们复习备考有着较好的导向作用. 测试反映的问题 【查看更多】

     

    题目列表(包括答案和解析)

    上海浦东有两建筑物A、B，由于建筑物中间有障碍物，无法丈量出它们之间的距离，请你在浦西不过江，利用斜三角形的知识，设计一个测量建筑物A、B间距离的方案，并给出具体的计算方法．

    查看答案和解析>>

    （2011•通州区一模）在一次知识竞赛中，共设计了“数理化类”、“人文类”、“天文地理类”三种类别的选择题共6个．如果从中任意抽取一个题，这个题是“数理化类”、“人文类”的概率分别是
    1
    2
    ，
    1
    3
    ．比赛时，每位选手从中一个个的不放回的抽取3个题目作答．
    （I）求“数理化类”、“人文类”、“天文地理类”各类试题的个数；
    （II）如果抽取的3个题目来自同一类别的概率为0.05，求抽取的3个题目来自完全不同类别的概率．

    查看答案和解析>>

           (本小题共〖2分)（注意:在试题卷上作答无效）

    某班拟从两名同学中选一人参加学校知识竞赛，现设计一个预选方案：选手从五道题中一次性随机抽取三道进行回答,已知甲五道题中只会三道，乙每道题答对的概率都是3/5,且每道题答对与否互不影响.

    (1) 分别求出甲乙两人答对题数的概率分布；

    (2) 你认为派谁参加比赛更合适.

     

    查看答案和解析>>

    在一次知识竞赛中，共设计了“数理化类”、“人文类”、“天文地理类”三种类别的选择题共6个．如果从中任意抽取一个题，这个题是“数理化类”、“人文类”的概率分别是
    1
    2
    ，
    1
    3
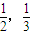    ．比赛时，每位选手从中一个个的不放回的抽取3个题目作答．
    （I）求“数理化类”、“人文类”、“天文地理类”各类试题的个数；
    （II）如果抽取的3个题目来自同一类别的概率为0.05，求抽取的3个题目来自完全不同类别的概率．

    查看答案和解析>>

    在一次知识竞赛中，共设计了“数理化类”、“人文类”、“天文地理类”三种类别的选择题共6个．如果从中任意抽取一个题，这个题是“数理化类”、“人文类”的概率分别是．比赛时，每位选手从中一个个的不放回的抽取3个题目作答．
    （I）求“数理化类”、“人文类”、“天文地理类”各类试题的个数；
    （II）如果抽取的3个题目来自同一类别的概率为0.05，求抽取的3个题目来自完全不同类别的概率．

    查看答案和解析>>


    同步练习册答案