练习册

  • 练习册
  • 试题
    设坐标平面上全部向量的集合为V.a=(a1.a2)为V的一个单位向量.已知从V到V的映射f由f(x)=-x+2(x·a)a(x∈V)确定. (1)若x.y∈V.求证:f(x)·f(y)=x·y, (2)对于x∈V.计算f［f(x)］-x, (3)设u=(1.0).v=(0.1).若f(u)=v.求a. (1)证明:f(x)·f(y)=［-x+2(x·a)a］·［-y+2(y·a)a］ =x·y-4(x·a)(y·a)+4(x·a)(y·a)a2=x·y. (2)解:∵f［f(x)］=f［-x+2(x·a)a］ =-［-x+2(x·a)a］+2{［-x+2(x·a)a］·a}a =x-2(x·a)a+2［-x·a+2(x·a)a2］a =x-2(x·a)a+2(x·a)a=x. ∴f［f(x)］-x=0. (3)解:由f(u)=v.得 解得或 ∴a=(.)或a=(-.-). 【查看更多】

     

    题目列表(包括答案和解析)

    设坐标平面上全部向量的集合为A，已知从A到A的映射f由f(x)＝x－2(x·a)a确定，其中x∈A，a＝(cos，sin)(∈R)．

    (1)当的取值发生变化时，f(f(x))的结果是否发生变化？请证明你的结论；

    (2)若|m|＝，|n|＝，f(f(m＋2n))与f(f(2m－n))垂直，求m与n的夹角．

    查看答案和解析>>

    （2010•南充一模）在坐标平面上直线l的方向向量
    e
    =(-
    4
    5
    ，
    3
    5
    )    ，点O（0，0），A（1，-2）在l上的正射影分别为O1、A1，设
    O1A1
    =λ
    e
    ，则实数λ=（　　）

    查看答案和解析>>

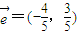    在坐标平面上直线l的方向向量，点O（0，0），A（1，-2）在l上的正射影分别为O1、A1，设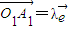，则实数λ=（ ）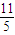
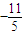
    A．2
    B．-2
    C．
    D．

    查看答案和解析>>

    在坐标平面上直线l的方向向量
    e
    =(-
    4
    5
    ，
    3
    5
    )    ，点O（0，0），A（1，-2）在l上的正射影分别为O1、A1，设
    O1A1
    =λ
    e
    ，则实数λ=（　　）
    A．2B．-2C．
    11
    5
    		D．-
    11
    5

    查看答案和解析>>

    设坐标平面上有三点A,B,C,ｉ,j分别是坐标平面上x轴、y轴正方向的单位向量,若向量=ｉ-2j,=ｉ＋ｍj,那么是否存在实数ｍ,使A,B,C三点共线.

    查看答案和解析>>


    同步练习册答案