(本小题满分12分)

在股票市场上，投资者常参考股价（每一股的价格）的某条平滑均线（记作MA）的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时，发现一只股票的MA均线近期走得很有特点：如果按如图所示的方式建立平面直角坐标系xoy，则股价y（元）和时间x的关系在ABC段可近似地用解析式来描述，从C点走到今天的D点，是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线对称。老赵预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线对称，EF段是股价延续DE段的趋势（规律）走到这波上升行情的最高点F。现在老赵决定取点，点，点来确定解析式中的常数，并且已经求得。

（1）请你帮老赵算出，并回答股价什么时候见顶（即求F点的横坐标）；

（2）老赵如能在今天以D点处的价格买入该股票5000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？

.（本小题满分12分）

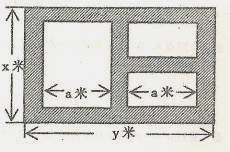
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周（阴影部分）为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S平方米.

（1）   分别写出用x表示y和S的函数关系式（写出函数定义域）

（2）   怎样设计能使s取得最大值，最大值为多少？

（本小题满分12分）

为了美化环境，构建两型社会，市城建局打算在广场上建造一个绚丽多彩的矩形花园，中间有三个完全一样的矩形花坛，每个花坛面积均为294平方米，花坛四周的过道均为

2米，如图所示，设矩形花坛的长为，宽为，整个矩形花园面积为

（1）试用表示S；

（2）为了节约用地，当矩形花坛的长为多少米时，新建矩形花园占地最少，占地多少平米？

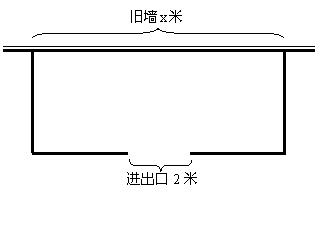
（本小题满分12分）围建一个面积为360平方米的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2米的进出口，如图所示，已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为米，工程总造价为(单位：元)。

（Ⅰ）将表示为的函数；    

（Ⅱ）试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用。

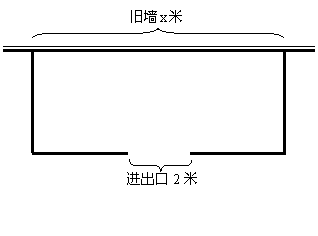
（本小题满分12分）围建一个面积为360平方米的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2米的进出口，如图所示，已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为米，工程总造价为(单位：元)。

（Ⅰ）将表示为的函数；    

（Ⅱ）试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用。