解：因为有负根，所以在y轴左侧有交点，因此

解：因为函数没有零点，所以方程无根，则函数y=x+|x-c|与y=2没有交点，由图可知c>2

 13．证明：（1）令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

（2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

数字1，2，3，4恰好排成一排，如果数字i（i=1，2，3，4）恰好出现在第i个位置上则称有一个巧合，求巧合数的分布列。

如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED．
（Ⅰ）求证：BD⊥平面POA；
（Ⅱ）当PB取得最小值时，请解答以下问题：
（i）求四棱锥P-BDEF的体积；
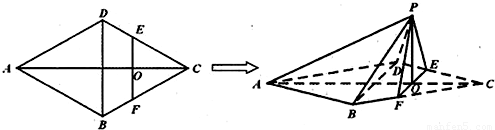
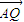（ii）若点Q满足=λ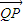 （λ＞0），试探究：直线OQ与平面PBD所成角的大小是否一定大于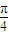？并说明理由．

（本小题满分12分）

为了解某班学生喜欢打篮球是否与性别有关，对该班50人进行了问卷调查得到了如下的列联表：

	喜欢打篮球	不喜欢打篮球	合 计
男 生		5
女 生	10
合 计			50

已知在全部50人中随机抽取1人抽到喜欢打篮球的学生的概率为0.6。

（Ⅰ）请将上面的列联表补充完整；

（Ⅱ）是否有99％的把握认为喜欢打篮球与性别有关？说明你的理由；

（Ⅲ）已知不喜欢打篮球的5位男生中，喜欢踢足球，喜欢打羽毛球，喜欢打乒乓球，现在从这5位男生中选取3位进行其他方面的调查，求和不全被选中的概率。

附:1．

2．在统计中，用以下结果对变量的独立性进行判断：

(1)当时,没有充分的证据判定变量有关联，可以认为变量是没有关联的；

(2)当时，有90%的把握判定变量有关联；

(3)当时，有95%的把握判定变量有关联；

(4)当时，有99%的把握判定变量有关联。

 

 

 

 

 

（本小题满分12分）

为了解某班学生喜欢打篮球是否与性别有关，对该班50人进行了问卷调查得到了如下的列联表：

	喜欢打篮球	不喜欢打篮球	合 计
男 生		5
女 生	10
合 计			50

已知在全部50人中随机抽取1人抽到喜欢打篮球的学生的概率为0.6。

（Ⅰ）请将上面的列联表补充完整；

（Ⅱ）是否有99％的把握认为喜欢打篮球与性别有关？说明你的理由；

（Ⅲ）已知不喜欢打篮球的5位男生中，喜欢踢足球，喜欢打羽毛球，喜欢打乒乓球，现在从这5位男生中选取3位进行其他方面的调查，求和不全被选中的概率。

附:1．

2．在统计中，用以下结果对变量的独立性进行判断：

(1)当时,没有充分的证据判定变量有关联，可以认为变量是没有关联的；

(2)当时，有90%的把握判定变量有关联；

(3)当时，有95%的把握判定变量有关联；

(4)当时，有99%的把握判定变量有关联。