
题目列表(包括答案和解析)
| 1 |
| 10 |
| A、0 | B、1 | C、2 | D、3 |
设函数f1(x)=![]() ,f2(x)=x-1,f3(x)=x2,则f1(f2(f3(2 013)))=________.
,f2(x)=x-1,f3(x)=x2,则f1(f2(f3(2 013)))=________.
思路 本题是一个三次复合函数![]() 求值问题,首先求f3(2 013),在此基础上求f2,f1.
求值问题,首先求f3(2 013),在此基础上求f2,f1.
(1)(u±v)′= ;?
(2)(uv)′= ;?
(3)(![]() )′= ;?
)′= ;?
(4)设函数u=φ(x)在点x处有导数ux′=φ′(x),函数y=![]() 在点x的对应点u处有导数yu′=
在点x的对应点u处有导数yu′=![]() ,则复合函数y=f[φ(x)]在点x处有导数且yx′= .
,则复合函数y=f[φ(x)]在点x处有导数且yx′= .
今有一组数据如下:
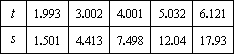
现准备用下列函数的一个近似地表示数据所满足的规律,其中最接近的一个是
s=2t-3-1
s=![]()
s=![]()
s=-2t-2
下列命题中真命题是
[
]A
.函数的最大值一定是函数的极大值B
.函数的极大值可能会小于这个函数的极小值C
.函数在某一闭区间上的极小值就是函数在这一区间上的最小值D
.函数在开区间内不存在最大值和最小值湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com