练习册

  • 练习册
  • 试题
    20． 某厂有保留下来的一面旧墙长28米.现准备利用这面旧墙的一段为一面墙.建造平面 图形为矩形.面积为504平方米的厂房.工程的条件是: (Ⅰ)修1米旧墙的费用是造1米新墙费用的25%, (Ⅱ)拆去旧墙1米用所得材料建1米新墙费用是造1米新墙费用的50%, (Ⅲ)建门窗的费用与建新墙的费用相同.因此不再考虑. 问如何利用旧墙才能使建墙费用最低. 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)

    某厂有一面旧墙长14米,现在准备利用这面旧墙建造平面图形为矩形,面积为126平方米的厂房,工程条件是①建1米新墙费用为a元；②修1米旧墙的费用为元；③拆去1米旧墙,用所得材料建1米新墙的费用为元,经过讨论有两种方案: (1)利用旧墙的一段x米（x＜14）为矩形厂房一面的边长；(2)矩形厂房利用旧墙的一面边长x≥14.问如何利用旧墙,即x为多少米时,建墙费用最省?(1)、(2)两种方案哪个更好?

     

    查看答案和解析>>

    某工厂有14m长的旧墙一面，现在准备利用这面旧墙，建造平面图形为矩形，面积为126m2的厂房，工程条件为：①建1m新墙的费用为a元；②修1m旧墙的费用为
    a
    4
    元；③拆去1m旧墙，用所得材料建造1m新墙的费用为
    a
    2
    元．经过讨论有两种方案：
    （Ⅰ）利用旧墙的一段xm（x＜14）为矩形厂房一面的边长；
    （Ⅱ）矩形厂房利用旧墙的一面边长为x（x≥14）．
    问：如何利用旧墙，即x为多少米时，建墙费用最省？（Ⅰ）（Ⅱ）两种方案哪个更好？

    查看答案和解析>>

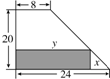    某厂有形状为直角梯形的边角料，现从中截取矩形铁片（如图示），当矩形面积最大时，矩形的两边x，y分别应为
    15，12
    15，12
    ．

    查看答案和解析>>

    （2006•东城区三模）某厂有一台价值为1万元的生产设备，现要通过技术改造来提高该生产设备的生产能力，提高产品的增加值，经过市场调查，产品的增加值y万元与技术改造投入金额x万元之间满足：①y与（1-x）和x2的乘积成正比；②当x=
    1
    2
    时，y=
    1
    2
    ．并且技术改造投入的金额满足；
    x
    2(1-x)
    ∈（0，t]，其中t为常数．
    （1）求y=f（x）的解析式及定义域；
    （2）当t∈（0，2]时，求产品的增加值的最大值及相应的技术改造投入的金额．

    查看答案和解析>>

    某仓库有同样规格的产品12箱，其中6箱、4箱、2箱依次是由甲、乙、丙三个厂生产的，且三个厂的次品率分别是
    1
    10
    ，
    1
    14
    ，
    1
    18
    ．现从这12箱中任取一箱，再从取得的一箱中任意取出一个产品．
    （1）求取得的一件产品是次品的概率；（2）若已知取得一件产品是次品，问这个次品是乙厂生产的概率是多少？

    查看答案和解析>>


    同步练习册答案