
题目列表(包括答案和解析)
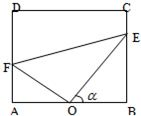 某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25| 3 |
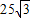 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.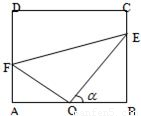
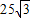 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.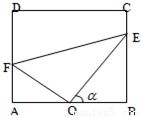
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com