(本小题满分12分)

是否存在实数p，使4x+P < 0是的充分条件?　如果存在，求出p的取值范围；若不存在，说明理由．

已知抛物线，过定点作两条互相垂直的直线，若与抛物线交于点，与抛物线交于点，的斜率为.某同学已正确求得弦的中点坐标为，请写出弦的中点坐标           ．

 

在估计总体分布时，我们常常画出样本的频率分布直方图或频率折线图，如果样本容量无限增大，分组的组距无限减小，那么频率折线图就会无限接近于总体密度曲线，请查阅有关资料，了解总体密度曲线的意义和作用．

意大利数学家斐波那契(L.　Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定每对大兔子每月能生一对小兔子,而每对小兔子过了一个月就可长成大兔子,如果不发生死亡,那么由一对大兔子开始,一年后能有多少对大兔子呢??

我们依次给出各个月的大兔子对数,并一直推算下去到无尽的月数,可得数列:?

1,1,2,3,5,8,13,21,34,55,89,144,233,….?

这就是斐波那契数列,此数列中a₁=a₂=1,你能归纳出,当n≥3时a_n的递推关系式吗??

      

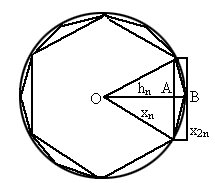
如图，设圆的半径为1，弦心距为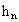；正n边形的边长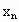为，面积为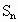．由勾股定理，得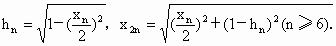

　　容易知道．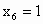

　　观察图1，不难发现，正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积，即

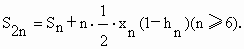
利用这个递推公式，我们可以得到：

正六边形的面积

正十二边形的面积________；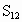

正二十四边形的面积________；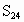

…

请问n的输入值满足什么条件？n的输出组表示什么？当n不断增大，的值不断趋近于什么？用循环结构编写出程序，还用Scilab语言编写一个程序．