练习册

  • 练习册
  • 试题
    2．考查学生的数学探究能力 指出:数学是研究空间形式和数量关系的科学.是刻画自然规律和社会规律的科学语言和有效工具.数学教学使学生掌握数学的基础知识.基本技能.基本思想.使学生表达清晰.思考有条理.使学生具有实事求是的态度.锲而不舍的精神.使学生学会用数学的思考方式解决问题.认识世界. 例7(2005北京春季高考第20题) 现有一组互不相同且从小到大排列的数据:a0.a1.a2.a3.a4.a5.其中a0＝0.为提取反映数据间差异程度的某种指标.今对其进行如下加工:记T＝a0+a1+a2+a3+a4+a5.xn＝.yn＝(a0+a1+-+an).作函数y＝f(x).使其图象为逐点依次连接点Pn(xn.yn)的折线. 的值, (2)设Pn-1Pn的斜率为kn.判断k1.k2.k3.k4.k5的大小关系, 时.f(x)＜x, (4)求由函数y＝x与y＝f(x)的图象所围成图形的面积S(用a1.a2.a3.a4.a5表示). 本题以数字为研究对象.波及的知识点多.这点对于学生来说.具有一定的挑战性.但更具有值挑战性的是.学生要有勇气.毅力和探究能力. 【查看更多】

     

    题目列表(包括答案和解析)

    下列调查中哪些是用普查的方式，哪些是用抽样调查的方式来收集数据的？

    (1)某市教育部门为了了解全市初中学生的视力情况，选择城区的一所初中和农村的一所初中，对这两所学校的全体学生进行检查；

    (2)某厂的一台车床每天加工3 000个零件．为了掌握零件的质量，每天选取其中的100个进行相关项目的质量测试；

    (3)某校为了调查本校高中学生的数学应用能力，对全校的高中学生进行书面和实践两方面测试；

    (4)某工厂为了掌握全厂工人的身体健康状况，请一家医院对全厂工人进行体检；

    (5)为了测定一种铜丝的最大控断力，在一批铜丝中取50根进行测试．

    查看答案和解析>>

    已知某校5个学生的数学和物理成绩如下表：
    学生的编号i 1 2 3 4 5
    数学xi 80 75 70 65 60
    物理yi 70 66 68 64 62
    （Ⅰ）通过大量事实证明发现，学生的数学成绩和物理成绩具有很强的线性相关关系，用x表示数学成绩，用y表示物理成绩，根据上述表格求y与x的回归方程；
    （Ⅱ）利用残差分析回归方程的拟合效果，若残差和在（-0.1，0.1）范围内，则称回归方程为“优拟方程”，问：该回归方程是否为“优拟方程”？
    参考公式和数据：回归直线方程：
    ?
    y
    =bx+a    ，其中b=
    n
    i=1
    xiyi-n
    .
    x
    •
    .
    y
    n
    i=1
    x
    2
    i
    -n
    .
    x
    2
    ，a=
    .
    y
    -b
    .
    x
    ；
    5
    i=1
    xiyi=23190，
    5
    i=1
    x
    2
    i
    =24750    ，残差和公式为：
    5
    i=1
    (yi-
    ?
    y
    i    )    ．

    查看答案和解析>>

    某地区甲校高二年级有1100人，乙校高二年级有900人，为了统计两个学校高二年级在学业水平考试中的数学学科成绩，采用分层抽样的方法在两校共抽取了200名学生的数学成绩，如下表：（已知本次测试合格线是50分，两校合格率均为100%）
    甲校高二年级数学成绩：
    分组 [50，60） [60，70） [70，80） [80，90） [90，100]
    频数 10 25 35 30 x
    乙校高二年级数学成绩：
    分组 [50，60） [60，70） [70，80） [80，90） [90，100]
    频数 15 30 25 y 5
       （I）计算x，y的值，并分别估计以上两所学校数学成绩的平均分（精确到1分）
    （II）若数学成绩不低于80分为优秀，低于80分为非优秀，根据以上统计数据写下面2×2列联表，并回答能否在犯错误的概率不超过0.05的前提下认为“两个学校的数学成绩有差异？”
    甲校 乙校 总计
    优秀
    非优秀
    总计
    附：
    P（K2≥k0） 0.10 0.05 0.025 0.010 0.005
    k0 2.706 3.841 5.024 6.635 7.879
    k2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ．

    查看答案和解析>>

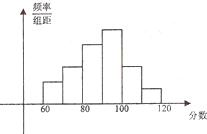    精英家教网为了解高三学生的数学学习情况，现抽取某班60名学生的数学成绩进行分析，将所得数据整理后，画出其频率分布直方图（如图）．已知从左到右各长方形高的比为2：3：5：6：3：1，则该班学生数学成绩在（80，100）之间的学生人数是
     

    查看答案和解析>>

    调查某校100名学生的数学成绩情况，得下表：
    一般 良好 优秀
    男生（人） x 18 y
    女生（人） 10 17 z
    已知从这批学生中随机抽取1名学生，抽到成绩一般的男生的概率为0.15．
    （1）求x的值；
    （2）若用分层抽样的方法，从这批学生中随机抽取20名，问应在优秀学生中抽多少名？
    （3）已知y≥17，z≥18，优秀学生中男生不少于女生的概率．

    查看答案和解析>>


    同步练习册答案