
题目列表(包括答案和解析)
| 3 |
 已知2008年某省经教育部批准自主命题高考题,为慎重起见,该省提前制定了两套方案,且对这两套方案在全省14个地级市分别召集专家进行研讨,并对认为合理的方案进行了投票表决,统计结果如茎叶图所示,试说明方案比较稳妥的是
已知2008年某省经教育部批准自主命题高考题,为慎重起见,该省提前制定了两套方案,且对这两套方案在全省14个地级市分别召集专家进行研讨,并对认为合理的方案进行了投票表决,统计结果如茎叶图所示,试说明方案比较稳妥的是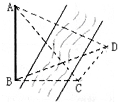 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使在C塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔高AB的高度为( )
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使在C塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔高AB的高度为( ) 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=60米,并在点C测得塔顶A的仰角为60°,则塔高AB=( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=60米,并在点C测得塔顶A的仰角为60°,则塔高AB=( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com