练习册

  • 练习册
  • 试题
    排列与组合.概率与统计是高中数学的重要内容．一方面.这部分内容占用教学时数多达36课时.另一方面.这部分内容是进一步学习高等数学的基础知识.因此.它是高考数学命题的重要内容．从近三年全国高考数学试题来看.主要是考查排列与组合.概率与统计的基本概念.公式及基本技能.方法.以及分析问题和解决问题的能力．试题特点是基础和全面．题目类型有选择题.填空题.解答题.一般是两小.解答题通常是概率问题．试题难度多为低中档．为了支持高中数学课程的改革.高考数学命题对这部分将进一步重视.但题目数量.难度.题型将会保持稳定． 例1．在一块并排10垄的田地中.选择2垄分别种植A.B两种作物.每种作物种植一垄.为有利于作物生长.要求A.B两种作物间的间隔不小于6垄.则不同的选垄方法共有 种． [解析] A种植在左边第一垄时.B有3种不同的种植方法, A种植在左边第二垄时.B有两种不同的种植方法, A种植在左边第三垄时.B只有一种种植方法． B在左边种植的情形与上述情形相同． 故共有2=12种不同的选垄方法． ∴ 应填12. 例2．将3种作物种植在如图所示的5块试验田里.每一块种植一种作物且相邻的试验田不能种植同一作物.不同的种植方法共有 种． [解析] 将5块试验田从左到右依次看作甲.乙.丙.丁.戊.3种作物依次看作A.B.C.则3种作物都可以种植在甲试验田里.由于相邻的试验田不能种植同一种作物.从而可知在乙试验田里只能有两种作物．同理.在丙.丁.戊试验田里也只能有两种作物可以种植． 由分步计数原理.不同的种植方法共有3×2×2×2=48种． ∴应填:48 例3．某城市中心广场建造一个花圃.花圃分为6个部分.现要栽种4种不同颜色的花.每部分栽种1种且相邻部分不能栽种同样颜色的花.不同的栽法有 种． [解析] 由于第1.2.3块两两相邻.我们先安排这三块.给第1.2.3块种花时分别有4.3.2种种法.所以共有4×3×2=24种不同种法． 下面给第4块种花.若第4块与第6块同色.只有一种种植方法.则第5块只有2种种法.若第4块与第2块同色时.共有2×1=2种种法． 若第4块与第6块不同色.但第4块与第2块同色.则第6块有2种种植的方案.而第5块只有1种种法.共有2种不同的种植方法． 若第4块与第6块不同色.但第4块与第2块不同色.则第6块有1种种法.则第5块也有一种不同种法.所以第4块与第6块不同色时.有1种种法． 综上共有24×=120种不同的种植方法． 例4．某班新年联欢会原定的5个节目已排成节目单.开演前又增加了两个新节目.如果将这两个节目插入原节目单中.那么不同的插法的种数为 A.42 B.30 C.20 D.12 [解析] 将两个新节目插入5个固定顺序节目单有两种情况: (1)两个新节目相邻的插法种数为, (2)两个节目不相邻的插法种数为,由分类计数原理共有种方法.选A. 例5． 设甲.已.丙三人每次射击命中目标的概率分别为0.7.0.6和0.5. (1)三人各向目标射击一次.求至少有一人命中目标的概率及恰有两人命中目标的概率, (2)若甲单独向目标射击三次.求他恰好命中两次的概率. 解:(I)设AK表示“第k人命中目标 .k=1.2.3. 这里.A1.A2.A3独立.且P(A1)=0.7.P(A2)=0.6.P(A3)=0.5. 从而.至少有一人命中目标的概率为 恰有两人命中目标的概率为 答:至少有一人命中目标的概率为0.94.恰有两人命中目标的概率为0.44 (II)设甲每次射击为一次试验.从而该问题构成三次重复独立试验.又已知在每次试验中事件“命中目标 发生的概率为0.7.故所求概率为 答:他恰好命中两次的概率为0.441. 例6．某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5. (Ⅰ)求至少3人同时上网的概率; (Ⅱ)至少几人同时上网的概率小于0.3 ? 分析: (Ⅰ)至少3人同时上网的概率等于1减去至多2人同时上网的概率.即 (Ⅱ)至少4人同时上网的概率为: .至少5人同时上网的概率为: 因此, 至少5人同时上网的概率小于0.3. 思路:如果在1次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生K次的概率为. 例7． 甲.乙.丙三台机床各自独立地加工同一种零件.已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲.丙两台机床加工的零件都是一等品的概率为. (Ⅰ)分别求甲.乙.丙三台机床各自加工零件是一等品的概率, (Ⅱ)从甲.乙.丙加工的零件中各取一个检验.求至少有一个一等品的概率. 解:(Ⅰ)设A.B.C分别为甲.乙.丙三台机床各自加工的零件是一等品的事件. ① ② ③ 由题设条件有 由①.③得 代入②得 27[P(C)]2-51P(C)+22=0. 解得 . 将 分别代入 ③.② 可得 即甲.乙.丙三台机床各加工的零件是一等品的概率分别是 (Ⅱ)记D为从甲.乙.丙加工的零件中各取一个检验.至少有一个一等品的事件. 则 故从甲.乙.丙加工的零件中各取一个检验.至少有一个一等品的概率为 【查看更多】

     

    题目列表(包括答案和解析)

    排列与组合的联系与区别

    (1)排列和组合都是从n个不同元素中取出m(m≤n)个元素，但排列与元素的顺序_________，而组合与元素的顺序_________；

    (2)排列数与组合数的关系：_________．

    查看答案和解析>>

    有一个公用电话亭，在观察使用这个电话的人的流量时，设在某一时刻有n个人正在使用电话或等待使用的概率为P（n），且P（n）与时刻t无关，统计得到P(n)=
    (
    1
    2
    )n•P(0)(1≤n≤3)
    0(n≥4)
    那么在某一时刻，这个公用电话亭里一个人也没有的概率是
     
    ．

    查看答案和解析>>

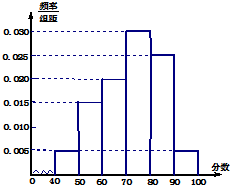    精英家教网某校从高一年级期中数学考试的学生中抽出60名学生，学生的成绩均为整数，并把成绩分成六组，作出了成绩频率分布直方图如图所示．
    （1）求这次考试的及格率（60分及以上为及格）；
    （2）求这次考试成绩的中位数与平均数，并说明这次考试成绩中位数与平均数大小关系的统计意义；
    （3）从成绩是70分以上的学生中选两人，求他们在同一组的概率．

    查看答案和解析>>

    （2005•武汉模拟）有一个公用电话亭，在观察使用这个电话的人的流量时，设在某一时刻，有n个人正在使用电话或等待使用的概率为P（n），且P（n）与时刻t无关，统计得到P（n）=
    (
    1
    2
    )n•P(0)1≤n≤5
    0n≥6
    ，那么在某一时刻，这个公用电话亭时一个人也没有的概率P（0）的值是
    32
    63
    32
    63
    ．

    查看答案和解析>>

    为调查中学生近视情况，测得某校男生150名中有80名近视，女生140名中有70名近视．在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力（　　）

    查看答案和解析>>


    同步练习册答案