练习册

  • 练习册
  • 试题
    (一) 选择题 1.1∥2.a.b与1.2都垂直.则a.b的关系是 A.平行 B.相交 C.异面 D.平行.相交.异面都有可能 2.异面直线a.b.a⊥b.c与a成300.则c与b成角范围是 A.[600.900] B.[300.900] C.[600.1200] D.[300.1200] 3.正方体AC1中.E.F分别是AB.BB1的中点.则A1E与C1F所成的角的余弦值是 A. B. C. D. 4.在正△ABC中.AD⊥BC于D.沿AD折成二面角B-AD-C后.BC=AB.这时二面角B-AD-C大小为 A.600 B.900 C.450 D.1200 5.一个山坡面与水平面成600的二面角.坡脚的水平线为AB.甲沿山坡自P朝垂直于AB的方向走30m.同时乙沿水平面自Q朝垂直于AB的方向走30m.P.Q都是AB上的点.若PQ=10m.这时甲.乙2个人之间的距离为 A. B. C. D. 6.E.F分别是正方形ABCD的边AB和CD的中点.EF交BD于O.以EF为棱将正方形折成直二面角如图.则∠BOD= A.1350 B.1200 C.1500 D.900 7.三棱锥V-ABC中.VA=BC.VB=AC.VC=AB.侧面与底面ABC所成的二面角分别为α.β.γ.则cosα+cosβ+cosγ等于 A.1 B.2 C. D. 8.正n棱锥侧棱与底面所成的角为α.侧面与底面所成的角为β.tanα∶tanβ等于 A. B. C. D. 9.一个简单多面体的各面都是三角形.且有6个顶点.则这个简单多面体的面数是 A.4 B.6 C.8 D.10 10.三棱锥P-ABC中.3条侧棱两两垂直.PA=a.PB=b.PC=c.△ABC的面积为S.则P到平面ABC的距离为 A. B. C. D. 11.三棱柱ABC-A1B1C1的体积为V.P.Q分别为AA1.CC1上的点.且满足AP=C1Q.则四棱锥B-APQC的体积是 A. B. C. D. 12.多面体ABCDEF中.已知面ABCD是边长为3的正方形.EF∥AB.EF=.EF与面AC的距离为2.则该多面体的体积为 A. B.5 C.6 D. 【查看更多】

     

    题目列表(包括答案和解析)

    选择题．

    (1)为了得到函数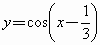的图像，只需将余弦函数图像上各点

    [　　]

    A．向左平移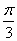个单位长度

    B．向右平移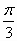个单位长度

    C．向左平移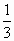个单位长度

    D．向右平移个单位长度

    (2)为了得到函数的图像，只需将函数的图像上各点(　　)即可．

    [　　]

    A．横坐标伸长为原来的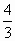倍，纵坐标不变

    B．横坐标缩短为原来的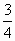倍，纵坐标不变

    C．纵坐标伸长为原来的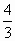倍，横坐标不变

    D．纵坐标缩短为原来的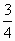倍，横坐标不变

    (3)将函数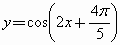的图像上各点向右平行移动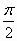个单位长度，再把横坐标缩短为原来的一半，纵坐标伸长为原来的4倍，则所得到的图像的函数解析式是

    [　　]

    A．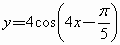

    B．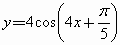

    C．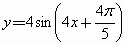

    D．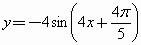

    查看答案和解析>>

    选择题．

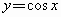
    (1)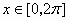，的图像与直线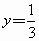的交点的个数为

    [　　]

    A．0

    B．1

    C．2

    D．3

    (2)当x∈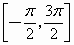时，函数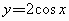

    [　　]

    A．在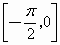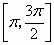，上是增加的，在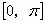上是减少的

    B．在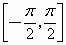上是增加的，在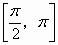上是减少的

    C．在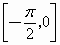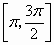，上是减少的，在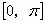上是增加的

    D．在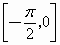∪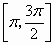上是增加的，在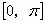上是减少的

    (3)下列命题中正确的是

    [　　]

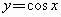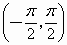    A．函数在上是减少的

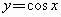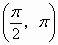    B．函数在上是减少的

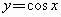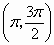    C．函数在上是减少的

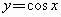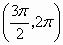    D．函数在上是减少的

    (4)函数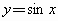和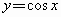都是增加的区间是

    [　　]

    A．

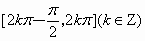
    B．

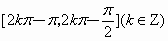
    C．

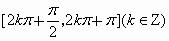
    D．

    查看答案和解析>>

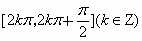
    选择题．

    (1)下列几何体中是棱柱的有

    [　　]

    (A)1个

    (B)2个

    (C)3个

    (D)4个

    (2)下列命题正确的是

    [　　]

    (A)有两个面平行，其余各面都是四边形的几何体叫棱柱．

    (B)有两个面平行，其余各面都是平行四边形的几何体叫棱柱．

    (C)有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱．

    (D)用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．

    (3)如下图，右边长方体中由左边的平面图形围成的是

    [　　]

    (4)充满气的车轮内胎可由下面某个图形绕对称轴旋转而成，这个图形是

    [　　]

    查看答案和解析>>

    选择题．

    (1)由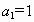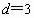，确定的等差数列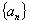，当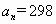时，序号n等于

    [　　］

    (A)99．

    (B)100．

    (C)96．

    (D)101．

    (2)一个蜂巢里有1只蜜蜂．第1天，它飞出去找回了5个伙伴；第2天，6只蜜蜂飞出去，各自找回了5个伙伴……如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢中一共有(　　)只蜜蜂．

    [　　]

    (A)55986．

    (B)46656．

    (C)216．

    (D)36．

    (3)预测人口的变化趋势有多种方法，“直接推算法”使用的公式是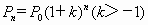，其中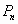为预测期人口数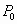，为初期人口数，k为预测期内年增长率，n为预测期间隔年数．如果在某一时期有－1＜k＜0，那么在这期间人口数

    [　　]

    (A)呈上升趋势．

    (B)呈下降趋势．

    (C)摆动变化．

    (D)不变．

    (4)《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的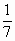是较小的两份之和，问最小1份为

    [　　]

    (A)．

    (B)．

    (C)．

    (D)．

    查看答案和解析>>

    选择题：

    (1)已知，，，则

    [　　]

    (A)A、B、D三点共线

    (B)A、B、C三点共线

    (C)B、C、D三点共线

    (D)A、C、D三点共线

    (2)已知正方形ABCD的边长为1，，，，则等于

    [　　]

    (A)0

    (B)3

    (C)

    (D)

    (3)已知，，，，且四边形ABCD为平行四边形，则

    [　　]

    (A)a＋b＋c＋d＝0

    (B)a－b＋c－d＝0

    (C)a＋b－c－d＝0

    (D)a－b－c＋d＝0

    (4)已知D、E、F分别是△ABC的边BC、CA、AB的中点，且，，，则①；②；③；④

    中正确的等式的个数为

    [　　]

    (A)1

    (B)2

    (C)3

    (D)4

    (5)若，是夹角为60°的两个单位向量，则；的夹角为

    [　　]

    (A)30°

    (B)60°

    (C)120°

    (D)150°

    (6)若向量a、b、c两两所成的角相等，且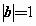，，，则等于

    [　　]

    (A)2

    (B)5

    (C)2或5

    (D)或

    (7)等边三角形ABC的边长为1，，，，那么a·b＋b·c＋c·a等于

    [　　]

    (A)3

    (B)－3

    (C)

    (D)

    查看答案和解析>>


    同步练习册答案