练习册

  • 练习册
  • 试题
    (三) 解答题 17.如图.在斜边为AB的直角三角形ABC中.过A作AP⊥平面ABC.AE⊥PB于E.AF⊥PC于F.CG⊥AB于G.CD⊥PB于D. 求△AEF面积的最大值. 18.等边三角形ABC的边长为a.沿平行BC的线段PQ折起.使平面APQ⊥平面PBCQ.设点A到直线PQ的距离为x.AB的长为d (1)x为何值时.d2取得最小值.最小值是多少?(2)若∠BAC=θ.求cosθ的最小值. 19.如图.ABCD是矩形.其4个顶点在平面α的同一侧.且它们在平面α内的射影分别为A’.B’.C’.D’.直线A’B与C’D’不重合. (1)求证:A’B’C’D’是平行四边形, (2)在怎样的条件下.A’B’C’D’是矩形?并证明你的结论. 20.正三棱锥V-ABC的底面边长为a.侧棱与底面所成的角等于θ(θ>).过底面一边作此棱锥的截面.当截面与底面所成二面角为何值时.截面面积最小?并求出最小值. 【查看更多】

     

    题目列表(包括答案和解析)

    方程组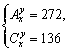的解是（　）

    A．x＝17，y＝2　　　　　　 B．x＝-16，y＝2

    C．x＝16，y＝2　　　　　　 D．x＝17，y＝16

     

    查看答案和解析>>

    由等式x4＋a1x3＋a2x2＋a3x＋a4＝(x＋1)4＋b1(x＋1)3＋b2(x＋1)2＋b3(x＋1)＋b4的定义映射f：(a1，a2，a3，a4)→b1＋b2＋b3＋b4，则f(4，3，2，1)＝

    [　　]

    A．10
    B．7
    C．－1
    D．0

    查看答案和解析>>

    已知三次函数f(x)＝x(x－a)(x－b)　　0＜a＜b

    (1)当f(x)取得极值时x＝s和x＝t(s＜t)，求证：o＜s＜a＜t＜b；

    (2)求f(x)的单调区间．

    查看答案和解析>>

    设a、b为正数，求证：不等式＋1＞　①成立的充要条件是：对于任意实数x＞1，有ax＋＞b　②．

    查看答案和解析>>

    解答题：解答应写出文字说明，证明过程或演算步骤．

    已知函数　g(x)＝x

    (1)

    若干x＞1，求证：

    (2)

    是否存在实数k，是方程有四个不同的实根？若存在，求出k的取值范围；若不存在，说明理由．

    查看答案和解析>>


    同步练习册答案