练习册

  • 练习册
  • 试题
    数学中的常量和变量相互依存.并在一定条件下相互转化．而参数是介于常量和变量之间的具有中间性质的量.它的本质是变量.但又可视为常数.正是由于参数的这种两重性和灵活性.在分析和解决问题的过程中.引进参数就能表现出较大的能动作用和活力.“引参求变 是一种重要的思维策略.是解决各类数学问题的有力武器． 参数广泛地存在于中学的数学问题中.比如:代数中.函数的解析式.数列的通项公式,含参数的方程或不等式,解析几何中含参数的曲线方程和曲线的参数方程等等． 参数是数学中的活泼“元素 .特别是一个数学问题中条件与结论涉及的因素较多.转换过程较长时.参数的设定和处理的作用尤为突出.合理选用参数.并处理好参数与常数及变数的联系与转换.在某些问题的求解过程中起到了十分关键的作用． 【查看更多】

     

    题目列表(包括答案和解析)

    下列关于赋值语句的说法正确的是（    ）

    A.赋值语句中赋值号“=”与数学中的等号的含义是相同的

    B.赋值后左右两边可以交换，例如a=b和b=a的作用是一样的

    C.赋值语句可以将一个含有变量的自身的代数式的值再赋给这个变量

    D.赋值语句可以用来进行代数式的演算

    查看答案和解析>>

    某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作．比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩．假设每个运动员完成每个系列中的K和D两个动作的得分是相互独立的．根据赛前训练的统计数据，某运动员完成甲系列和乙系列中的K和D两个动作的情况如下表：

    现该运动员最后一个出场，之前其他运动员的最高得分为115分．

    (1)若该运动员希望获得该项目的第一名，应选择哪个系列？说明理由．并求其获得第一名的概率．

    (2)若该运动员选择乙系列，求其成绩ξ的分布列及数学期望Eξ．

    查看答案和解析>>

    下列关于赋值语句的说法正确的是

    [     ]

    A.赋值语句中“=”与数学中的等号含义是相同的
    B.赋值语句中“=”左右两边可以交换，如a=b和b=a的作用是一样的
    C.赋值语句可以将一个含有变量自身的代数式的值再赋给这个变量
    D.赋值语句可以用来进行代数式的演算

    查看答案和解析>>

    某班学生在一次数学考试中成绩分布如下表：
    分数 [0，80） [80，90） [90，100） [100，110） [110，120） [120，130） [130，140） [140，150]
    人数 2 5 6 8 12 6 4 2
    那么分数在[100，110）中的频率和分数不满110分的累积频率分别是
     
    （精确到0.01）．

    查看答案和解析>>

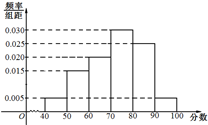    精英家教网某校从参加高三年级期末统考测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
    （Ⅰ）估计这次测试数学成绩的平均分和众数；
    （Ⅱ）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为ξ，求ξ的分布列及数学期望Eξ．

    查看答案和解析>>


    同步练习册答案