
题目列表(包括答案和解析)
(本小题满分12分)
已知0<a<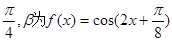 的最小正周期,
的最小正周期,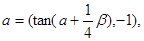 求
求 .
.
(本小题满分12分)
已知函数f(x)=Asin(![]() x+
x+![]() )(A>0,
)(A>0, ![]() >0,|
>0,|![]() |<
|<![]() ) (x∈R)的部分图象如图所示.
) (x∈R)的部分图象如图所示.
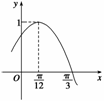 (1)求f(x)的表达式;
(1)求f(x)的表达式;
(2)设g(x)=f(x)-![]() f
f![]() ,求函数g(x)的最小值及相应的x的取值集合.
,求函数g(x)的最小值及相应的x的取值集合.
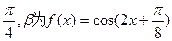 的最小正周期,
的最小正周期, 求
求 .
.()(本小题满分12分)
已知0<a<![]() 的最小正周期,
的最小正周期,![]() 求
求![]() .
.
(本题满分12分)
 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,∣φ∣<
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,∣φ∣<![]() ,x∈R)的图象的一部分如下图
,x∈R)的图象的一部分如下图
所示.
(1)求函数f(x)的解析式;
(2)求函数y=f(x)+f(x+2)的最大值与最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com