题目列表(包括答案和解析)
设函数h(x)＝x2，
(x)＝2elnx(e为自然对数的底)．
(1)求函数F(x)＝h(x)－x的极值；
(2)若存在常数k和b，使得函数f(x)和g(x)对其定义域内的任意实数x分别满足f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为函数f(x)和g(x)的“隔离直线”．试问：函数h(x)和(x)是否存在“隔离直线”？若存在，求出“隔离直线”方程；若不存在，请说明理由．
(1)设x、y、z1∈R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
(2)设二次函数f(x)＝ax2＋bx＋c(a＞0)，方程f (x)－x＝0有两个实根x1，x2，且满足：0＜x1＜x2＜
，若x∈(0，x1)．
求证：x＜f(x)＜x1
（12分）（1）设x、y、z
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
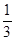（2）设二次函数f (x)＝ax2＋bx＋c （a＞0），方程f (x)－x＝0有两个实根x1，x2，
且满足：0＜x1＜x2＜
，若x(0，x1)。
求证：x＜f (x)＜x1
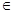R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
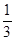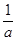，若x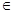(0，x1)。设集合s为非空实数集，若数
满足：（1）对
有
，即是S的上界（下界）：（2）对
，使得xo >a（xo <a），即是S的最小（最大）上界（下界），则称数为数集S的上（下）确界，记作
．给出如下命题：
① 若 S = {x|x2 < 2} ，则 supS =－
；
② 若S={x|x=n|，x∈N}，则infS=l
③ 若A、B皆为非空有界数集，定义数集A+B={z|z=x+y, x
，y∈B}，则
sup（A+B）= sup A+supB
其中正确的命题的序号为 （填上所有正确命题的序号）．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com