
题目列表(包括答案和解析)
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问
题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、
四轮问题的概率分别为 、
、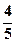 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问
题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、
四轮问题的概率分别为 、
、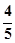 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
【解析】本试题主要考查了二次方程根的问题的综合运用。运用反证法思想进行证明。
先反设,然后推理论证,最后退出矛盾。证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.显然不成立。
证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com